
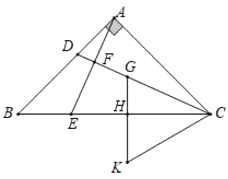
【题目】如图,等腰直角三角形![]() 中,
中,![]() ,D是
,D是![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() 交
交![]() 于
于![]() 在是
在是![]() 上一点,过点
上一点,过点![]() 作
作![]() 于
于![]() ,延长
,延长![]() 到
到![]() 连接
连接![]() ,使
,使![]() ,若
,若![]() ,则线段
,则线段![]() 的长度为_______.
的长度为_______.
【答案】![]()
【解析】
作高线AM,根据等腰直角三角形和三线合一得:∠BAM=∠CAM=45°,设∠BAE=α,表示各角的度数,证明KG=KC,由HG:HK=2:3,设HG=2a,HK=3a计算KC、KG和CH的长,根据等角三角函数得tan∠EAM=![]() ,设FN=b,则AF=2b,由勾股定理列方程得:AD2=AF2+DF2,得102=(2a)2+(
,设FN=b,则AF=2b,由勾股定理列方程得:AD2=AF2+DF2,得102=(2a)2+(![]() b)2,解出b的值可得结论.
b)2,解出b的值可得结论.
解:过点A作AM⊥BC于点M,交CD于点N,
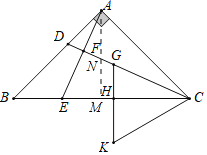
∴∠AMB=∠AMC=90°,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,AM=BM=CM,∠BAM=∠CAM=45°,
设∠BAE=α,则∠EAM=45°-α,∠AEC=∠B+∠BAE=45°+α,
∵AE⊥CD于点F,
∴∠AFD=∠AFC=∠EFC=90°,
∴∠ACF=90°-∠CAF=∠BAE=α,
∴∠ECF=∠ACB-∠ACF=45°-α=∠EAM,
∵GH⊥BC于H,
∴∠CHG=∠CHK=90°,
∴∠CGH=90°![]() ∠ECF=90°-(45°-α)=45°+α,∠K+∠KCH=90°,
∠ECF=90°-(45°-α)=45°+α,∠K+∠KCH=90°,
∵∠K+2∠BAE=90°,
∴∠KCH=2∠BAE=2α,
∴∠KCG=∠KCH+∠ECF=2α+(45°-α)=45°+α,
∴∠CGH=∠KCG,
∴KG=KC,
∵HG:HK=2:3,设HG=2a,HK=3a,
∴KC=KG=5a,
∴Rt△CHK中,CH=![]() ,
,
∴Rt△CHG中,tan∠ECF=![]() ,
,
∴Rt△CMN中,tan∠ECF=![]() ,
,
∴MN=![]() CM=
CM=![]() AM=AN,
AM=AN,
∵∠ECF=∠EAM=45°-α,
∴Rt△ANF中,tan∠EAM=![]() =
=![]() ,
,
设FN=b,则AF=2b,
∴MN=AN=![]() ,
,
∴AM=CM=2AN=![]() ,
,
∴Rt△CMN中,CN=![]() ,
,
∴CF=FN+CN=6b,
∴Rt△ACF中,tan∠ACF=![]() ,
,
∵∠ACF=∠DAF=α,
∴Rt△ADF中,tan∠DAF=![]() ,
,
∴DF=![]() AF=
AF=![]() b,
b,
∵AD2=AF2+DF2,AD=10,
∴102=(2a)2+(![]() b)2,
b)2,
解得:b1=![]() ,b2=
,b2=![]() (舍去),
(舍去),
∴CF=6×![]() =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】现今“微信运动”被越来越多的人关注和喜爱,某数学兴趣小组随机调查了我市![]() 名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

请根据以上信息,解答下列问题:
(1)写出![]() ,
,![]() ,
,![]() ,
,![]() 的值并补全频数分布直方图;
的值并补全频数分布直方图;
(2)我市约有![]() 名教师,用调查的样本数据估计日行走步数超过
名教师,用调查的样本数据估计日行走步数超过![]() 步(包含
步(包含![]() 步)的教师有多少名?
步)的教师有多少名?
(3)若在![]() 名被调查的教师中,选取日行走步数超过
名被调查的教师中,选取日行走步数超过![]() 步(包含
步(包含![]() 步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在
步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在![]() 步(包含
步(包含![]() 步)以上的概率.
步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆共有80间客房.宾馆负责人根据经验作出预测:今年7月份,每天的房间空闲数y(间)与定价x(元/间)之间满足y=![]() x﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为( )
x﹣42(x≥168).若宾馆每天的日常运营成本为5000元,有客人入住的房间,宾馆每天每间另外还需支出28元的各种费用,宾馆想要获得最大利润,同时也想让客人得到实惠,应将房间定价确定为( )
A.252元/间B.256元/间C.258元/间D.260元/间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是
是![]() 轴正半轴上的一个动点,以
轴正半轴上的一个动点,以![]() 为边作等腰直角
为边作等腰直角![]() ,使
,使![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,能表示
,能表示![]() 与
与![]() 的函数关系的图像( )
的函数关系的图像( )
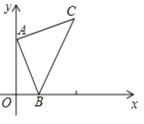
A.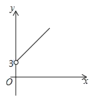 B.
B.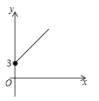 C.
C.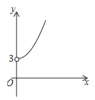 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,过点![]() 的两条直线分别交
的两条直线分别交![]() 轴于
轴于![]() ,
,![]() 两点,且
两点,且![]() 、
、![]() 两点的纵坐标分别是一元二次方程
两点的纵坐标分别是一元二次方程![]() 的两个根.
的两个根.
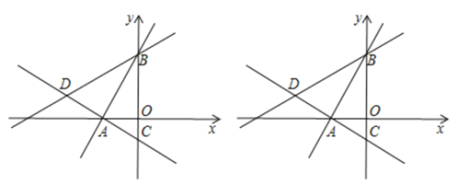
(1)试问:直线![]() 与直线
与直线![]() 是否垂直?请说明理由.
是否垂直?请说明理由.
(2)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,在直线![]() 上寻找点
上寻找点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰三角形,请直接写出
三点为顶点的三角形是等腰三角形,请直接写出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,![]() 是坐标原点,抛物线
是坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 两点(如图),顶点是
两点(如图),顶点是![]() ,对称轴交
,对称轴交![]() 轴于点
轴于点![]()
(1)如图(1)求抛物线的解析式;
(2)如图(2)![]() 是第三象限抛物线上一点,连接
是第三象限抛物线上一点,连接![]() 并延长交抛物线于点
并延长交抛物线于点![]() ,连接
,连接![]() 求证:
求证:![]() ;
;
(3)如图(3)在(2)问条件下,![]() 分别是线段
分别是线段![]() 延长线上一点,连接
延长线上一点,连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,若
,若![]()
![]()
![]() 求点
求点![]() 坐标.
坐标.
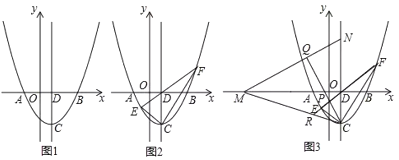
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN周长最小时,则∠AMN+∠ANM的度数是________
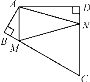
查看答案和解析>>
科目:初中数学 来源: 题型:
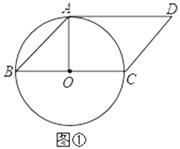
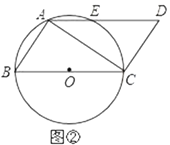
【题目】已知四边形ABCD是平行四边形,且以BC为直径的⊙O经过点A.
(1)如图①,若AD与⊙O相切,求∠ABC的度数;
(2)如图②,若AD与⊙O相交,交点E为AD的中点,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是线段
是线段![]() 上的两点,
上的两点,![]() ,
,![]() ,
,![]() .以
.以![]() 为圆心以
为圆心以![]() 为半径作圆弧,以
为半径作圆弧,以![]() 为圆心以
为圆心以![]() 为半径作圆弧,两圆弧相交于点
为半径作圆弧,两圆弧相交于点![]() 构成
构成![]() ,设
,设![]() .
.
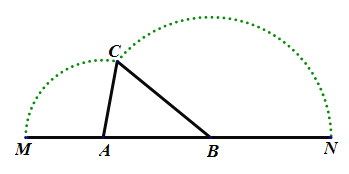
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() 为直角三角形,求
为直角三角形,求![]() 的值;
的值;
(3)当![]() 是锐角时,求
是锐角时,求![]() 的最大面积?
的最大面积?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com