
【题目】如图所示,在平面直角坐标系中,过点![]() 的两条直线分别交
的两条直线分别交![]() 轴于
轴于![]() ,
,![]() 两点,且
两点,且![]() 、
、![]() 两点的纵坐标分别是一元二次方程
两点的纵坐标分别是一元二次方程![]() 的两个根.
的两个根.
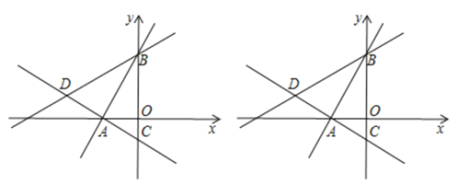
(1)试问:直线![]() 与直线
与直线![]() 是否垂直?请说明理由.
是否垂直?请说明理由.
(2)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,在直线![]() 上寻找点
上寻找点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 三点为顶点的三角形是等腰三角形,请直接写出
三点为顶点的三角形是等腰三角形,请直接写出![]() 点的坐标.
点的坐标.
【答案】(1)AC⊥AB,理由见解析(2)D的坐标为(2![]() ,1)(3)点P的坐标为(3
,1)(3)点P的坐标为(3![]() ,0),(
,0),(![]() ,2),(3,3
,2),(3,3![]() ),(3,3+
),(3,3+![]() )
)
【解析】
(1)求出方程x22x3=0的两个根得到OB,OC,由tan∠ABO=![]() ,tan∠ACO=
,tan∠ACO=![]() ,推出∠ABO=30°,∠ACO=60°,即可解决问题;
,推出∠ABO=30°,∠ACO=60°,即可解决问题;
(2)如图1中,过D作DE⊥x轴于E.由△ADE≌△ACO,推出DE=OC=1,AE=OA=![]() ,求出点D坐标;
,求出点D坐标;
(3)A、B、P三点为顶点的三角形是等腰三角形,可分为以下三种情况:①AB=AP;②AB=BP;③AP=BP;然后分别求出P的坐标即可.
(1)结论:AC⊥AB.理由如下:
∵由x22x3=0得:
∴x1=3,x2=1
∴B(0,3),C(0,1),
∵A(![]() ,0),B(0,3),C(0,1),
,0),B(0,3),C(0,1),
∴OA=![]() ,OB=3,OC=1,
,OB=3,OC=1,
∴tan∠ABO=![]() ,tan∠ACO=
,tan∠ACO=![]() ,
,
∴∠ABO=30°,∠ACO=60°,
∴∠BAC=90°,
∴AC⊥AB;
(2)如图1中,过D作DE⊥x轴于E.
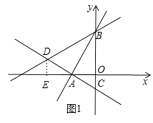
∴∠DEA=∠AOC=90°,
∵tan∠ACO=![]() ,
,
∵∠DCB=60°
∵DB=DC,
∴△DBC是等边三角形,
∵BA⊥DC,
∴DA=AC,
∵∠
在△ADE和△ACO中,
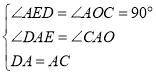 ,
,
∴△ADE≌△ACO,
∴DE=OC=1,AE=OA=![]()
∴OE=2![]() ,
,
∴D的坐标为(2![]() ,1);
,1);
(3)设直线BD的解析式为:y=mx+n,直线BD与x轴交于点E,
把B(0,3)和D(2![]() ,1)代入y=mx+n,
,1)代入y=mx+n,
∴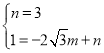 ,
,
解得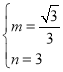 ,
,
∴直线BD的解析式为:y=![]() x+3,
x+3,
令y=0代入y=![]() x+3,
x+3,
∴x=3![]() ,
,
∴E(3![]() ,0),
,0),
∴OE=3![]() ,
,
∴tan∠BEC=![]() ,
,
∴∠BEO=30°,
同理可求得:∠ABO=30°,
∴∠ABE=30°,
当PA=AB时,如图2,
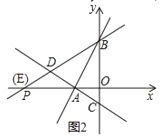
此时,∠BEA=∠ABE=30°,
∴EA=AB,
∴P与E重合,
∴P的坐标为(3![]() ,0),
,0),
当PA=PB时,如图3,
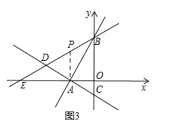
此时,∠PAB=∠PBA=30°,
∵∠ABE=∠ABO=30°,
∴∠PAB=∠ABO,
∴PA∥BC,
∴∠PAO=90°,
∴点P的横坐标为![]() ,
,
令x=![]() 代入y=
代入y=![]() x+3,
x+3,
∴y=2,
∴P(![]() ,2),
,2),
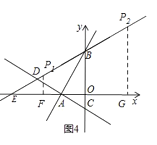
当PB=AB时,如图4,
∴由勾股定理可求得:AB=![]() =2
=2![]() ,EB=
,EB=![]() =6,
=6,
若点P在y轴左侧时,记此时点P为P1,
过点P1作P1F⊥x轴于点F,
∴P1B=AB=2![]() ,
,
∴EP1=62![]() ,
,
∴sin∠BEO=![]() ,
,
∴FP1=3![]() ,
,
令y=3![]() 代入y=
代入y=![]() x+3,
x+3,
∴x=3,
∴P1(3,3![]() ),
),
若点P在y轴的右侧时,记此时点P为P2,
过点P2作P2G⊥x轴于点G,
∴P2B=AB=2![]() ,
,
∴EP2=6+2![]() ,
,
∴sin∠BEO=![]() ,
,
∴GP2=3+![]() ,
,
令y=3+![]() 代入y=
代入y=![]() x+3,
x+3,
∴x=3,
∴P2(3,3+![]() ),
),
综上所述,当A、B、P三点为顶点的三角形是等腰三角形时,点P的坐标为(3![]() ,0),(
,0),(![]() ,2),(3,3
,2),(3,3![]() ),(3,3+
),(3,3+![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】![]() 年我国个人所得税征收办法最新规定:月收入不超过
年我国个人所得税征收办法最新规定:月收入不超过![]() 元的部分不收税;月收入超过
元的部分不收税;月收入超过![]() 元但不超过
元但不超过![]() 元的部分征收
元的部分征收![]() 的所得税;月收入超过
的所得税;月收入超过![]() 元但不超过
元但不超过![]() 元的部分征收
元的部分征收![]() 的所得税
的所得税![]() 国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入(专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用).如某人月工资收入
国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入(专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用).如某人月工资收入![]() 元,专项附加费支出
元,专项附加费支出![]() 元,他应缴纳个人所得税为:
元,他应缴纳个人所得税为:![]() (元).
(元).
(1)当月收入超过![]() 元而又不超过
元而又不超过![]() 元时,写出应缴纳个人所得税
元时,写出应缴纳个人所得税![]() (元)与月收入
(元)与月收入![]() (元)之间的关系式;
(元)之间的关系式;
(2)如果某人当月专项附加费支出![]() 元,缴纳个人所得税
元,缴纳个人所得税![]() 元,那么此人本月工资是多少元?
元,那么此人本月工资是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宜传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,将获得的数据整理绘制成如下两幅不完整的统计图.
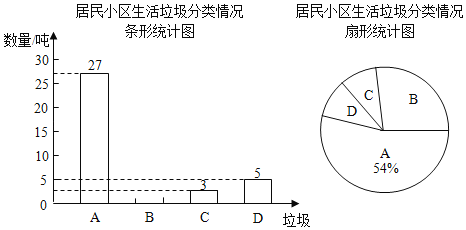
(注;A为可回收物,B为厨佘垃圾,C为有害垃圾,D为其它垃圾)
根据统计图提供的信息,解答下列问题:
(1)在这次抽样调查中,一共有 吨的生活垃圾;
(2)请将条形统计图补充完整;
(3)扇形统计图中,D所对应的圆心角度数是 .
(4)假设该城市每月产生的生活垃圾为5000吨,且全部分类处理,请估计每月产生的有害垃圾多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长为1的网格中,点![]() ,
,![]() ,
,![]() ,
,![]() 均在格点上,点
均在格点上,点![]() 是在直线
是在直线![]() 上的动点,连
上的动点,连![]() ,点
,点![]() 是点
是点![]() 关于直线
关于直线![]() 的对称点.
的对称点.
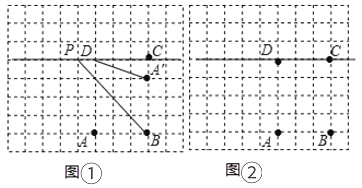
(1)在图①中,当![]() (点
(点![]() 在点
在点![]() 的左侧)时,计算
的左侧)时,计算![]() 的值等于______.
的值等于______.
(2)当![]() 取得最小值时,请在如图②所示的网格中,用无刻度的直尺画出点
取得最小值时,请在如图②所示的网格中,用无刻度的直尺画出点![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的.(不要求证明)
的位置是如何找到的.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数![]() 的图象经过点(1,-6).
的图象经过点(1,-6).
(1)求m的值;
(2)横、纵坐标都是整数的点叫做整点.记直线![]() 与反比例函数
与反比例函数![]() 的图象围成的区域为W(不含边界).若区域W内恰有1个整点,结合函数图象,直接写出b的取值范围.
的图象围成的区域为W(不含边界).若区域W内恰有1个整点,结合函数图象,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
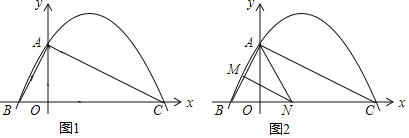
【题目】如图1,已知二次函数y=ax2+![]() x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
x+c(a≠0)的图象与y轴交于点A(0,4),与x轴交于点B、C,点C坐标为(8,0),连接AB、AC.
(1)请直接写出二次函数y=ax2+![]() x+c的表达式;
x+c的表达式;
(2)判断△ABC的形状,并说明理由;
(3)若点N在x轴上运动,当以点A、N、C为顶点的三角形是等腰三角形时,请写出此时点N的坐标;
(4)如图2,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求此时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市在创建全国文明城市过程中,决定购买A,B两种树苗对某路段道路进行绿化改造,已知购买A种树苗8棵,B种树苗3棵,需要950元;若购买A种树苗5棵,B种树苗6棵,则需要800元.
(1)求购买A,B两种树苗每棵各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于48棵,且用于购买这两种树的资金不能超过7500元,若购进这两种树苗共100棵,则有哪几种购买方案?
(3)某包工队承包种植任务,若种好一棵A种树苗可获工钱30元,种好一棵B种树苗可获工钱20元,在第(2)问的各种购买方案中,种好这100棵树苗,哪一种购买方案所付的种植工钱最少?最少工钱是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com