
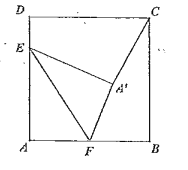
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() 为靠近点
为靠近点![]() 的四等分点,点
的四等分点,点![]() 为
为![]() 中点,将
中点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() 连接
连接![]() 则点
则点![]() 到
到![]() 所在直线距离为________________.
所在直线距离为________________.
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图在⊙O中,BC=2,AB=AC,点D为AC上的动点,且cosB=![]() .
.
(1)求AB的长度;
(2)求ADAE的值;
(3)过A点作AH⊥BD,求证:BH=CD+DH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民选择家用净水器,光明商场计划从生产厂家购进甲、乙两种型号的家用净水器,甲型号净水器进价为160元/台,乙型号净水器进价为280元/台,经过协商沟通,生产厂家拿出了两种优惠方案:第一种优惠方案:甲、乙两种型号净水器均按进价的8折收费;第二种优惠方案:甲型号净水器按原价收费,乙型号净水器的进货量超过10台后超过的部分按进价的6折收费.
光明商场只能选择一种优惠方案,已知光明商场计划购进甲型号净水器数量是乙型号净水器数量的1.5倍,设光明商场购进乙型号净水器![]() 台,选择第一种优惠方案所需费用为片
台,选择第一种优惠方案所需费用为片![]() 元,选择第二种优惠方案所需费用为
元,选择第二种优惠方案所需费用为![]() 元.
元.
(1)分别求出![]() 、
、![]() 与
与![]() 的关系式:
的关系式:
(2)光明商场计划购进乙型号净水器40台,请你为光明商场选择合适的优惠方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
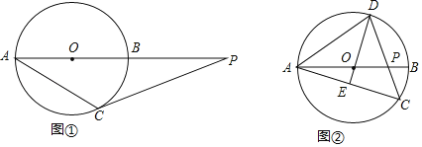
【题目】在⊙O中,AB为直径,C为⊙O上一点.
(Ⅰ)如图①,过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=32°,求∠P的大小;
(Ⅱ)如图②,D为优弧ADC上一点,且DO的延长线经过AC的中点E,连接DC与AB相交于点P,若∠CAB=16°,求∠DPA的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校小伟同学酷爱健身,一天去爬山锻炼,在出发点C处测得山顶部A的仰角为30度,在爬山过程中,每一段平路(CD、EF、GH)与水平线平行,每一段上坡路(DE、FG、HA)与水平线的夹角都是45度,在山的另一边有一点B(B、C、D同一水平线上),斜坡AB的坡度为2:1,且AB长为900![]() ,其中小伟走平路的速度为65.7米/分,走上坡路的速度为42.3米/分.则小伟从C出发到坡顶A的时间为( )(图中所有点在同一平面内
,其中小伟走平路的速度为65.7米/分,走上坡路的速度为42.3米/分.则小伟从C出发到坡顶A的时间为( )(图中所有点在同一平面内![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
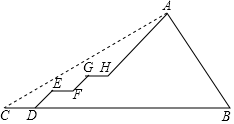
A.60分钟B.70分钟C.80分钟D.90分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知:在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() 分别在
分别在![]() 上,连接
上,连接![]() ,点
,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,则线段
,则线段![]() 与
与![]() 之间的数量关系是 ,位置关系是
之间的数量关系是 ,位置关系是

(2)如图2所示,已知:正方形![]() 将
将![]() 斜边
斜边![]() 的中点与点
的中点与点![]() 重合,直角顶点
重合,直角顶点![]() 落在正方形的
落在正方形的![]() 边上,
边上,![]() 的两直角边分别交
的两直角边分别交![]() 边于
边于![]() 两点(点
两点(点![]() 与点
与点![]() 重合),求证:
重合),求证:![]() ;
;
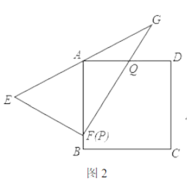
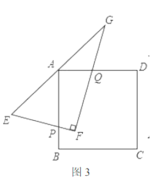
(3)如图3,若将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,两直角边分别交
,两直角边分别交![]() 边于
边于![]() 两点,如图3所示:判断四条线段
两点,如图3所示:判断四条线段![]() 之间是否存在什么确定的相等关系?若存在,证明你的结论.若不存在,请说明理由.
之间是否存在什么确定的相等关系?若存在,证明你的结论.若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】行驶中的汽车,在刹车后由于惯性的原因,还要继续向前滑行一段距离才能停住,这段距离称为“刹车距离”.为了测定某种型号汽车的刹车性能,对这种汽车的刹车距离进行测试,测得的数据如下表:
刹车时车速(千米/时) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
刹车距离(米) | 0 | 0.1 | 0.3 | 0.6 | 1 | 1.6 | 2.1 |
(1)在如图所示的直角坐标系中,以刹车时车速为横坐标,以刹车距离为纵坐标,描出这些数据所表示的点,并用平滑的曲线连结这些点,得到某函数的大致图象;
(2)测量必然存在误差,通过观察图象估计函数的类型,求出一个大致满足这些数据的函数表达式;
(3)一辆该型号汽车在高速公路上发生交通事故,现场测得刹车距离约为40米,已知这条高速公路限速100千米/时,请根据你确定的函数表达式,通过计算判断在事故发生时,汽车是否超速行驶.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com