
【题目】为提高饮水质量,越来越多的居民选择家用净水器,光明商场计划从生产厂家购进甲、乙两种型号的家用净水器,甲型号净水器进价为160元/台,乙型号净水器进价为280元/台,经过协商沟通,生产厂家拿出了两种优惠方案:第一种优惠方案:甲、乙两种型号净水器均按进价的8折收费;第二种优惠方案:甲型号净水器按原价收费,乙型号净水器的进货量超过10台后超过的部分按进价的6折收费.
光明商场只能选择一种优惠方案,已知光明商场计划购进甲型号净水器数量是乙型号净水器数量的1.5倍,设光明商场购进乙型号净水器![]() 台,选择第一种优惠方案所需费用为片
台,选择第一种优惠方案所需费用为片![]() 元,选择第二种优惠方案所需费用为
元,选择第二种优惠方案所需费用为![]() 元.
元.
(1)分别求出![]() 、
、![]() 与
与![]() 的关系式:
的关系式:
(2)光明商场计划购进乙型号净水器40台,请你为光明商场选择合适的优惠方案,并说明理由.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点D,E,F分别是△ABC三边的中点,则下列判断错误的是( )
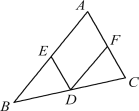
A. 四边形AEDF一定是平行四边形 B. 若AD平分∠A,则四边形AEDF是正方形
C. 若AD⊥BC,则四边形AEDF是菱形 D. 若∠A=90°,则四边形AEDF是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
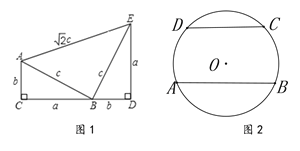
【题目】如图1,四边形ACDE是美国第二十任总统伽菲尔德验证勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知AE=![]() ,这时我们把关于x的形如
,这时我们把关于x的形如![]() 的一元二次方程称为“勾系一元二次方程”.
的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)判断方程![]() 是否是 “勾系一元二次方程”;并说明理由.
是否是 “勾系一元二次方程”;并说明理由.
(2)求证:关于![]() 的“勾系一元二次方程”
的“勾系一元二次方程” ![]() 必有实数根;
必有实数根;
(3)如图2,已知AB、CD是半径为5的⊙O的两条平行弦,AB=2a,CD=2b,a≠b,关于x的方程![]() 是“勾系一元二次方程”,求∠BAC的度数
是“勾系一元二次方程”,求∠BAC的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
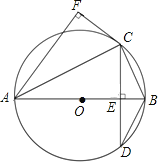
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A、B城往C、D两乡运肥料的平均费用如下表. 现C乡需要肥料240吨,D乡需要肥料260吨.
A城(出) | B城(出) | |
C乡(人) | 20元/吨 | 15元/吨 |
D乡(人) | 25元/吨 | 30元/吨 |
(1)A城和B城各多少吨肥料?
(2)设从B城运往D乡肥料x吨,总运费为y元,求y与x之间的函数关系,并写出自变量x的取值范围;
(3)由于更换车型,使B城运往D乡的运费每吨减少a元(a>0),其余路线运费不变,若C、D两乡的总运费最小值不少于10040元,求a的最大整数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,⊙O是正方形ABCD的外接圆,P是⊙O上不与A、B重合的任意一点,则∠APB等于( )
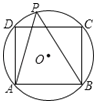
A.45° B.60° C.45° 或135° D.60° 或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是直线y=![]() +2与双曲线y=
+2与双曲线y=![]() 在第一象限内的一个交点,直线y=
在第一象限内的一个交点,直线y=![]() +2与x轴、y轴的交点分别为A、C,过P作PB⊥x轴,AB+PB=9.
+2与x轴、y轴的交点分别为A、C,过P作PB⊥x轴,AB+PB=9.
(1)求m的值;
(2)在双曲线上是否存在一点G,使得△ABG的面积等于△PBC的面积?若存在,求出点G的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD⊥CD,BC⊥CD,E为CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F。
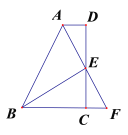
证明:(1)FC=AD;
(2)AB=BC+AD。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com