
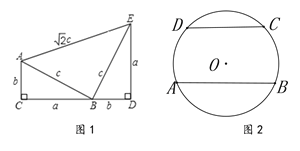
【题目】如图1,四边形ACDE是美国第二十任总统伽菲尔德验证勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知AE=![]() ,这时我们把关于x的形如
,这时我们把关于x的形如![]() 的一元二次方程称为“勾系一元二次方程”.
的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)判断方程![]() 是否是 “勾系一元二次方程”;并说明理由.
是否是 “勾系一元二次方程”;并说明理由.
(2)求证:关于![]() 的“勾系一元二次方程”
的“勾系一元二次方程” ![]() 必有实数根;
必有实数根;
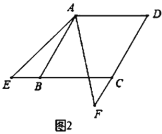
(3)如图2,已知AB、CD是半径为5的⊙O的两条平行弦,AB=2a,CD=2b,a≠b,关于x的方程![]() 是“勾系一元二次方程”,求∠BAC的度数
是“勾系一元二次方程”,求∠BAC的度数
【答案】(1)是,理由详见解析;(2)详见解析;(3)45°
【解析】
(1)根据“勾系一元二次方程”的定义即可判断;
(2)利用勾股定理以及“勾系一元二次方程”的定义即可解决问题;
(3)如图2中,连接OC,OB,作OE⊥CD于E,作EO的延长线交AB于F,利用全等三角形的性质推导出∠COB=90°即可解决问题.
(1)![]() 是 “勾系一元二次方程”,理由如下:
是 “勾系一元二次方程”,理由如下:
∵![]() 中,
中,![]()
∴![]()
∴![]() ,
,![]() 能构成直角三角形
能构成直角三角形
∴方程![]() 是“勾系一元二次方程”
是“勾系一元二次方程”
(2)∵关于![]() 的方程
的方程![]() 是“勾系一元二次方程”
是“勾系一元二次方程”
∴![]() 构成直角三角形,c是斜边
构成直角三角形,c是斜边
∴![]()
∵![]()
∴![]()
∴关于![]() 的“勾系一元二次方程”
的“勾系一元二次方程”![]() 必有实数根.
必有实数根.
(3)在图2中,连接OC,OB,作OE⊥CD于E,作EO的延长线交AB于F,如下图:

∵关于x的方程![]() 是“勾系一元二次方程”
是“勾系一元二次方程”
∴![]() ,5构成直角三角形,5是斜边
,5构成直角三角形,5是斜边
∴![]()
∵AB//CD,OE⊥CD
∴OF⊥AB
∴∠OEC=∠OFB= 90°
∴![]()
∵AB=2a,CD=2b
∴![]()
∵![]() ,
,
∴![]()
∴![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数![]() 都可以进行这样的分解,
都可以进行这样的分解,![]() (
(![]() ,
,![]() 是正整数且
是正整数且![]() ),在
),在![]() 的所有这种分解中,如果
的所有这种分解中,如果![]() ,
,![]() 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称![]() 是
是![]() 的最佳分解,并规定:
的最佳分解,并规定:![]() ,例如
,例如![]() 可以分解成
可以分解成![]() 、
、![]() 或
或![]() .因为
.因为![]() ,所有
,所有![]() 是最佳分解,所以
是最佳分解,所以![]() .
.
(1)求![]() .
.
(2)如果一个两位正整数![]() ,
,![]() (
(![]() ,
,![]() 、
、![]() 为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为
为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为![]() ,那么我们称这个数
,那么我们称这个数![]() 为 “吉祥数”,求所有“吉祥数”中
为 “吉祥数”,求所有“吉祥数”中![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
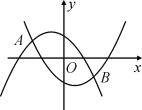
【题目】已知:如图所示的两条抛物线的解析式分别是y1=-ax2-ax+1,y2=ax2-ax-1(其中a为常数,且a>0).
(1)请写出三条与上述抛物线有关的不同类型的结论;
(2)当a=![]() 时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
时,设y1=-ax2-ax+1与x轴分别交于M,N两点(M在N的左边),y2=ax2-ax-1与x轴分别交于E,F两点(E在F的左边),观察M,N,E,F四点坐标,请写出一个你所得到的正确结论,并说明理由;
(3)设上述两条抛物线相交于A,B两点,直线l,l1,l2都垂直于x轴,l1,l2分别经过A,B两点,l在直线l1,l2之间,且l与两条抛物线分别交于C,D两点,求线段CD的最大值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在⊙O中,BC=2,AB=AC,点D为AC上的动点,且cosB=![]() .
.
(1)求AB的长度;
(2)求ADAE的值;
(3)过A点作AH⊥BD,求证:BH=CD+DH.

查看答案和解析>>
科目:初中数学 来源: 题型:
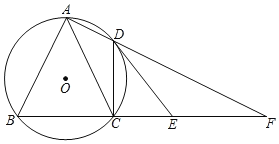
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°,AD、BC的延长线交于点F,点E在CF上,且∠DEC=∠BAC.
(1)求证:DE是⊙O的切线;
(2)若AB=AC,CE=10,EF=14,求CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,菱形ABCD中,AB=5,∠ABC=60°,∠EAF=60°,∠EAF的两边分别交BC、CD于E、F.
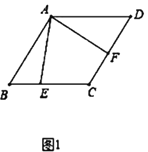
(1)如图1所示,当点E、F分别在边BC、CD上时,求CE+CF的值;
(2)如图2所示,当点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 的延长线时,请从
的延长线时,请从![]() ,
,![]() 两题中任选一题作答,我选______题.
两题中任选一题作答,我选______题.
![]() 题:则
题:则![]() 的值是________.
的值是________.
![]() 题:则
题:则![]() 与
与![]() 的关系是________.
的关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为表彰在“了不起我的国”演讲比赛中获奖的选手,决定购买甲、乙两种图书作为奖品.已知购买30本甲种图书,50本乙种图书共需1350元;购买50本甲种图书,30本乙种图书共需1450元.
(1)求甲、乙两种图书的单价分别是多少元?
(2)学校要求购买甲、乙两种图书共40本,且甲种图书的数量不少于乙种图书数量的![]() ,请设计最省钱的购书方案.
,请设计最省钱的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民选择家用净水器,光明商场计划从生产厂家购进甲、乙两种型号的家用净水器,甲型号净水器进价为160元/台,乙型号净水器进价为280元/台,经过协商沟通,生产厂家拿出了两种优惠方案:第一种优惠方案:甲、乙两种型号净水器均按进价的8折收费;第二种优惠方案:甲型号净水器按原价收费,乙型号净水器的进货量超过10台后超过的部分按进价的6折收费.
光明商场只能选择一种优惠方案,已知光明商场计划购进甲型号净水器数量是乙型号净水器数量的1.5倍,设光明商场购进乙型号净水器![]() 台,选择第一种优惠方案所需费用为片
台,选择第一种优惠方案所需费用为片![]() 元,选择第二种优惠方案所需费用为
元,选择第二种优惠方案所需费用为![]() 元.
元.
(1)分别求出![]() 、
、![]() 与
与![]() 的关系式:
的关系式:
(2)光明商场计划购进乙型号净水器40台,请你为光明商场选择合适的优惠方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.

(1)求证:BG=DE;
(2)若E为AD中点,FH=2,求菱形ABCD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com