
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=![]() ,求
,求![]() 的值.
的值.
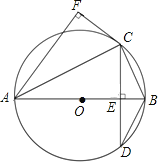
【答案】(1)证明:连接OC.
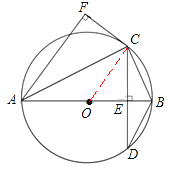
∵CE⊥AB,CF⊥AF,CE=CF,
∴AC平分∠BAF,即∠BAF=2∠BAC。
∵∠BOC=2∠BAC,∴∠BOC=∠BAF。
∴OC∥AF。∴CF⊥OC。∴CF是⊙O的切线。
(2)解:∵AB是⊙O的直径,CD⊥AB,
∴CE=ED,∠ACB=∠BEC=90°。
∴S△CBD=2S△CEB,∠BAC=∠BCE。∴△ABC∽△CBE。
∴![]() 。∴
。∴![]() 。
。
【解析】
(1)首先连接OC,由CD⊥AB,CF⊥AF,CF=CE,即可判定AC平分∠BAF,由圆周角定理即可得∠BOC=2∠BAC,则可证得∠BOC=∠BAF,即可判定OC∥AF,即可证得CF是⊙O的切线。
(2)由垂径定理可得CE=DE,即可得S△CBD=2S△CEB,由△ABC∽△CBE,根据相似三角形的面积比等于相似比的平方,易求得△CBE与△ABC的面积比,从而可求得![]() 的值。
的值。


科目:初中数学 来源: 题型:
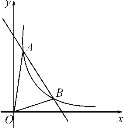
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1) 求一次函数的表达式;
(2) 根据图象写出kx+b-![]() <0的x的取值范围.
<0的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售某种品牌的手机,每部进货价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8部;而当销售价每降低50元时,平均每天就能多售出4部.
(1)当售价为2800元时,这种手机平均每天的销售利润达到多少元?
(2)若设每部手机降低x元,每天的销售利润为y元,试写出y与x之间的函数关系式.
(3)商场要想获得最大利润,每部手机的售价应订为为多少元?此时的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
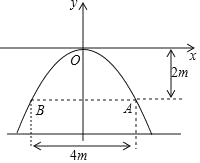
【题目】有一个截面的边缘为抛物线的拱桥桥洞,桥洞壁离水面AB的最大高度是2米,水面宽度AB为4米.把截面图形放在如图所示的平面直角坐标系中.
(1)求这条抛物线对应的函数表达式.
(2)若水面下降1米,求水面宽度增加了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省湖州市)如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
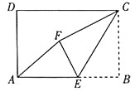
【题目】如图,在矩形 ![]() 中,
中, ![]() ,点
,点 ![]() 为线段
为线段 ![]() 上的动点,将
上的动点,将 ![]() 沿
沿 ![]() 折叠,使点
折叠,使点 ![]() 落在矩形内点
落在矩形内点 ![]() 处.下列结论正确的是________. (写出所有正确结论的序号)
处.下列结论正确的是________. (写出所有正确结论的序号)
①当 ![]() 为线段
为线段 ![]() 中点时,
中点时, ![]() ;②当
;②当 ![]() 为线段
为线段 ![]() 中点时,
中点时, ![]() ;
;
③当 ![]() 三点共线时,
三点共线时, ![]() ;④当
;④当 ![]() 三点共线时,
三点共线时, ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是
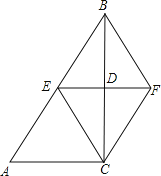
A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com