
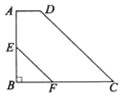
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F,求EF的长.
【答案】![]()
【解析】
可过点D作DG⊥BC于点G,解直角三角形DGC,求出DG=AB的长,进一步求出BE,再解直角三角形BEF,再解这个三角形即可;或延长FE交DA的延长线于点G,证明四边形DGFC是平行四边形,再证明△AGE≌△BFE,说明AG=BF,最后解依据DG=FC得出的一元一次方程即可.
解:如图1,过点D作DG⊥BC于点G,
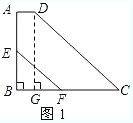
∵AD∥BC,∠B=90°,
∴∠A=90度.
可得四边形ABGD为矩形.
∴BG=AD=1,AB=DG.
∵BC=4,
∴GC=3.
∵∠DGC=90°,∠C=45°,
∴∠CDG=45°.
∴DG=GC=3.
∴AB=3.
又∵E为AB中点,
∴BE=![]() AB=
AB=![]() .
.
∵EF∥DC,
∴∠EFB=45°.
在△BEF中,∠B=90°.
∴EF=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
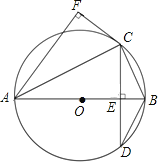
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为点E,CF⊥AF,且CF=CE.
(1)求证:CF是⊙O的切线;
(2)若sin∠BAC=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的四个顶点分别在反比例函数y=![]() 与y=
与y=![]() (x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)当m=4,n=20时.
①若点P的纵坐标为2,求直线AB的函数表达式.
②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
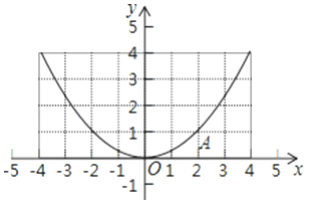
【题目】如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),
(1)求出二次函数的表达式;
(2)我们把横、纵坐标都为整数的点称为整点,请用整数n表示这条抛物线上所有的整点坐标.
(3)过y轴的正半轴上一点C(0,a)作AO的平行线交抛物线于点B,
①求出直线BC的函数表达式(用a表示);
②如果点B是整点,求证:△OAB的面积是偶数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD是水平的,BC与水平面的夹角为60°,其中AB=60cm,CD=40cm,BC=40cm,那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为___________cm
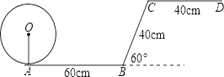
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,设两数![]() (
(![]() , 是常数,
, 是常数,![]() ).若函数
).若函数![]() 的图象过
的图象过![]() ,且
,且![]() .
.
(1)求![]() 的值:
的值:
(2)将函数![]() 的图象向上平移
的图象向上平移![]() 个单位,平移后的函数图象与函数
个单位,平移后的函数图象与函数![]() 的图象交于直线
的图象交于直线![]() 上的同一点,求
上的同一点,求![]() 的值;
的值;
(3)已知点![]() (
(![]() 为常数)在函数
为常数)在函数![]() 的图象上,
的图象上,![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,函数
,函数![]() 的图象经过点
的图象经过点![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“机动车行驶到斑马线要礼让行人”等交通法规实施后,某校数学课外实践小组就对这些交通法规的了解情况在全校随机调查了部分学生,调查结果分为四种:A.非常了解,B.比较了解,C.基本了解,D.不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.
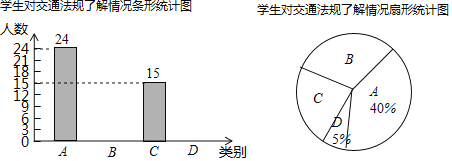
请结合图中所给信息解答下列问题:
(1)本次共调查 名学生;扇形统计图中C所对应扇形的圆心角度数是 ;
(2)补全条形统计图;
(3)该校共有800名学生,根据以上信息,请你估计全校学生中对这些交通法规“非常了解”的有多少名?
(4)通过此次调查,数学课外实践小组的学生对交通法规有了更多的认识,学校准备从组内的甲、乙、丙、丁四位学生中随机抽取两名学生参加市区交通法规竞赛,请用列表或画树状图的方法求甲和乙两名学生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学用配方法解方程x2+ax=b2时,方程的两边加上_____,据欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是:画Rt△ABC,使∠ACB=90°,BC=![]() ,AC=b,再在斜边AB上截取BD=
,AC=b,再在斜边AB上截取BD=![]() .则该方程的一个正根是线段_____的长.
.则该方程的一个正根是线段_____的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润![]() 元与精加工的蔬菜吨数
元与精加工的蔬菜吨数![]() 之间的函数关系式;
之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com