
【题目】小明同学用配方法解方程x2+ax=b2时,方程的两边加上_____,据欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是:画Rt△ABC,使∠ACB=90°,BC=![]() ,AC=b,再在斜边AB上截取BD=
,AC=b,再在斜边AB上截取BD=![]() .则该方程的一个正根是线段_____的长.
.则该方程的一个正根是线段_____的长.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是
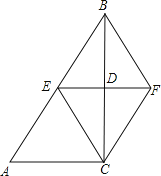
A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD>AB,点P是CD边上的任意一点(不含C,D两端点),过点P作PF∥BC,交对角线BD于点F.
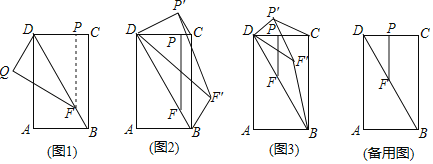
(1)如图1,将△PDF沿对角线BD翻折得到△QDF,QF交AD于点E.求证:△DEF是等腰三角形;
(2)如图2,将△PDF绕点D逆时针方向旋转得到△P'DF',连接P'C,F'B.设旋转角为α(0°<α<180°).
①若0°<α<∠BDC,即DF'在∠BDC的内部时,求证:△DP'C∽△DF'B.
②如图3,若点P是CD的中点,△DF'B能否为直角三角形?如果能,试求出此时tan∠DBF'的值,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=33°,则∠B的大小是( )
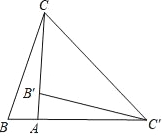
A. 33° B. 45° C. 57° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级举行毕业典礼,需要从九年(1)班的2名男生1名女生(男生用A1表示,女生用B1表示)和九年(2)班的1名男生1名女生(男生用A2表示,女生用B2表示)共5人中随机选出2名主持人.
(1)用树状图或列表法列出所有可能情形;
(2)求2名主持人来自不同班级的概率;
(3)求2名主持人恰好1男1女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com