
【题目】已知二次函数的图象的顶点为A(2,-2),并且经过B(1,0),C(3,0),求这条抛物线的函数表达式.
【答案】y=2x2-8x+6.
【解析】
由于二次函数的图象的顶点为A(2,-2),可设二次函数的表达式为y=a(x-2)2-2;
再运用图象经过点B(1,0),,C(3,0),将点B或者点C的坐标代入所设函数表达式即可求出a的值,进而求解,或者设一般式,把三个点的坐标带入求值即可.
解:解法1:设二次函数表达式为y=ax2+bx+c,将A(2,-2),B(1,0),C(3,0)代入,得
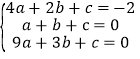 解得
解得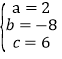 所以y=2x2-8x+6.
所以y=2x2-8x+6.
解法2:设二次函数表达式为y=a(x-2)2-2,将B(1,0)代入,得0=a(1-2)2-2,解得a=2.所以y=2(x-2)2-2,即y=2x2-8x+6.
解法3:设二次函数表达式为y=a(x-1)(x-3),将A(2,-2)代入,得-2=a(2-1)(2-3),解得a=2.所以y=2(x-1)(x-3),即y=2x2-8x+6.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
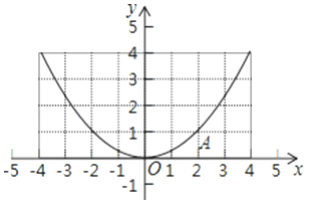
【题目】如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),
(1)求出二次函数的表达式;
(2)我们把横、纵坐标都为整数的点称为整点,请用整数n表示这条抛物线上所有的整点坐标.
(3)过y轴的正半轴上一点C(0,a)作AO的平行线交抛物线于点B,
①求出直线BC的函数表达式(用a表示);
②如果点B是整点,求证:△OAB的面积是偶数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学用配方法解方程x2+ax=b2时,方程的两边加上_____,据欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是:画Rt△ABC,使∠ACB=90°,BC=![]() ,AC=b,再在斜边AB上截取BD=
,AC=b,再在斜边AB上截取BD=![]() .则该方程的一个正根是线段_____的长.
.则该方程的一个正根是线段_____的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)停车难已成为合肥城市病之一,主要表现在居住停车位不足,停车资源结构性失衡,中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图,汽车靠墙一侧OB与墙MN平行且距离为0.8米,已知小汽车车门宽AO为 1.2 米,当车门打开角度∠AOB为40°时,车门是否会碰到墙?请说明理由.(参考数据:sin 40°≈0.64,cos 40°≈0.77,tan 40°≈0.84)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润![]() 元与精加工的蔬菜吨数
元与精加工的蔬菜吨数![]() 之间的函数关系式;
之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,

(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某城市对居民生活用水按以下规定收取每月的水费:家庭月用水量如果不超过8吨,按每吨2.5元收费;如果超过8吨,未超过的部分仍按每吨2.5元收取,而超过部分则按每吨4元收取.
(1)设某家庭月用水量为x吨,水费为y元,请写出y与x之间的函数解析式,并在给定的平面直角坐标系中,画出该函数的图象;
(2)如果小明家按题中规定今年3月份应缴水费34元,那么今年3月份小明家用水多少吨?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com