
【题目】(1)因式分解:![]() ___________.
___________.
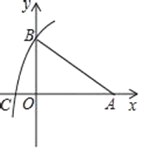
(2)如图,在平面直角坐标系中,A(6,0),B(0,2![]() ),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为_______.扇形BAC的面积为______.
),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为_______.扇形BAC的面积为______.
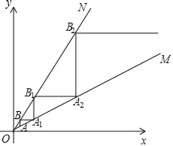
(3)在平面直角坐标系中,点![]() 在射线OM上,点
在射线OM上,点![]() 在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,则点B1的纵坐标为________,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_______.
在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,则点B1的纵坐标为________,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_______.
【答案】b(a+1)(a-1) (6-4![]() ,0) 4π 4 22021
,0) 4π 4 22021
【解析】
(1)先提取公因式b,再对余下的多项式利用平方差公式继续分解.
(2)根据勾股定理求出AB,根据坐标与图形性质求得OC的长即可求得点C的坐标,然后求得∠BAO的度数,利用扇形面积公式计算即可.
(3)根据题意,分别找到AB、A1B1、A2B2……及 BA1、B1A2、B2A3……线段长度递增规律即可
(1)a2b-b=b(a2-1)=b(a+1)(a-1).
故答案为:b(a+1)(a-1).
(2)由题意得,OB=2![]() ,OA=6,
,OA=6,
∴AB=![]() ,
,
则AC=4![]() ,
,
∴OC=AC-OA=4![]() -6,
-6,
∴点C坐标为(6-4![]() ,0),
,0),
∵tanA=![]() ,
,
∴∠A=30°,
∴S扇形ABC=![]() =4π,
=4π,
故答案为:(6-4![]() ,0),4π.
,0),4π.
(3)由已知可知
点A、A1、A2、A3……A2020各点在正比例函数y=![]() x的图象上
x的图象上
点B、B1、B2、B3……B2020各点在正比例函数y=![]() x的图象上
x的图象上
两个函数相减得到横坐标不变的情况下两个函数图象上点的纵坐标的差为![]() x ①;
x ①;
当A(B)点横坐标为![]() 时,由①AB=1,则BA1=
时,由①AB=1,则BA1=![]() ,则点A1横坐标为
,则点A1横坐标为![]() +
+![]() =2
=2![]() ,B1点纵坐标为
,B1点纵坐标为![]() 2
2![]() =4=22;
=4=22;
当A1(B1)点横坐标为2![]() ,由①A1B1=2,则B1A2=2
,由①A1B1=2,则B1A2=2![]() ;则点A2横坐标为2
;则点A2横坐标为2![]() +2
+2![]() =4
=4![]() ,B2点纵坐标为
,B2点纵坐标为![]() ×4
×4![]() =8=23;
=8=23;
当A2(B2)点横坐标为4![]() ,由①A2B2=4,则B2A3=4
,由①A2B2=4,则B2A3=4![]() ,则点A3横坐标为4
,则点A3横坐标为4![]() +4
+4![]() =8
=8![]() ,B3点纵坐标为
,B3点纵坐标为![]() ×8
×8![]() =16=24;
=16=24;
依稀类推
点B2020的纵坐标为22021
故答案为4,22021.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
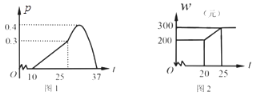
【题目】某农作物的生长率P与温度t(℃)有如下关系:如图1,当10≤t≤25时可近似用函数![]() 刻画;当25≤t≤37时可近似用函数
刻画;当25≤t≤37时可近似用函数![]() 刻画.
刻画.
(1)求h的值.
(2)按照经验,该作物提前上市的天数m(天)与生长率P满足函数关系:
生长率P | 0.2 | 0.25 | 0.3 | 0.35 |
提前上市的天数m(天) | 0 | 5 | 10 | 15 |
①请运用已学的知识,求m关于P的函数表达式;
②请用含![]() 的代数式表示m ;
的代数式表示m ;
(3)天气寒冷,大棚加温可改变农作物生长速度.在(2)的条件下,原计划大棚恒温20℃时,每天的成本为200元,该作物30天后上市时,根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此给大棚继续加温,加温后每天成本w(元)与大棚温度t(℃)之间的关系如图2.问提前上市多少天时增加的利润最大?并求这个最大利润(农作物上市售出后大棚暂停使用).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,且
边上一点,且![]() .点
.点![]() 是直线
是直线![]() 上一点且在点
上一点且在点![]() 的右侧,
的右侧,![]() ,点
,点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向以每秒1个单位长度的速度运动,设运动时间为
方向以每秒1个单位长度的速度运动,设运动时间为![]() 秒.以
秒.以![]() 为圆心,
为圆心,![]() 为半径作半圆
为半径作半圆![]() ,交直线
,交直线![]() 分别于点
分别于点![]() ,
,![]() (点
(点![]() 在
在![]() 的左侧).
的左侧).
(1)当![]() 秒时,
秒时,![]()
![]() 的长等于__________,
的长等于__________,![]() __________秒时,半圆
__________秒时,半圆![]() 与
与![]() 相切;
相切;
(2)当点![]() 与点
与点![]() 重合时,求半圆
重合时,求半圆![]() 被矩形
被矩形![]() 的对角线
的对角线![]() 所截得的弦长;
所截得的弦长;
(3)若![]() ,求扇形
,求扇形![]() 的面积.
的面积.
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,将点P沿着y轴翻折,得到的对应点再沿着直线l翻折得到点P1,则P1称为点P的“l变换点”.
(1)已知:点P(1,0),直线l:x=2,求点P的“l变换点”的坐标;
(2)若点Q和它的“l变换点”Q1的坐标分别为(2,1)和(3,2),求直线l的解析式;
(3)如图,⊙O的半径为2.
①若⊙O上存在点M,点M的“l变换点”M1在射线![]() x(x≥0)上,直线l:x=b,求b的取值范围;
x(x≥0)上,直线l:x=b,求b的取值范围;
②将⊙O在x轴上移动得到⊙E,若⊙E上存在点N,使得点N的“l变换点”N1在y轴上,且直线l的解析式为y=![]() x+1,求E点横坐标的取值范围.
x+1,求E点横坐标的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区一种商品的需求量y1(单位:万件)、供应量y2(单位;万件)与价格x(单位:元/件)分别近似满足下列函数关系式:y1=-x+60,y2=2x-36.需求量为0时,即停止供应.当y1=y2时,该商品的价格称为稳定价格,需求量称为稳定需求量.
(1)求该商品的稳定价格与稳定需求量;
(2)价格在什么范围时,该商品的需求量低于供应量;
(3)当需求量高于供应量时,政府常通过对供应方提供价格补贴来提高供货价格,以提高供应量.现若要使稳定需求量增加4万件,政府应对每件商品提供多少元补贴才能使供应量等于需求量?
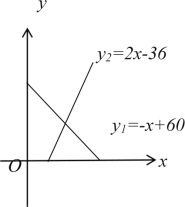
查看答案和解析>>
科目:初中数学 来源: 题型:
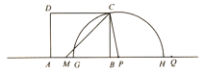
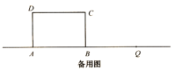
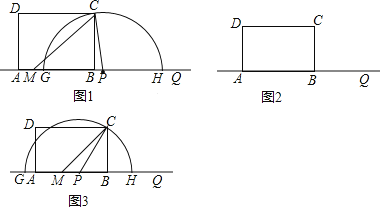
【题目】如图,在矩形ABCD中,AB=4,BC=3.点M是AB边上一点,且∠CMB=45°.点Q是直线AB上一点且在点B的右侧,BQ=4,点P从点Q出发,沿射线QA方向以每秒2个单位长度的速度运动,设运动时间为t秒.以P为圆心,PC长为半径作半圆P,交直线AB分别于点G,H(点G在点H的左侧).
(1)当t=1秒时,PC的长为 ,t= 秒时,半圆P与AD相切;
(2)当点P与点B重合时,求半圆P被矩形ABCD的对角线AC所截得的弦长;
(3)若∠MCP=15°,请直接写出扇形HPC的弧长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:将一个大于0的自然数,去掉其个位数字,再把剩下的数加上原数个位数字的4倍,如果得到的和能被13整除,则称这个数是“一刀两断”数,如果和太大无法直接观察出来,就再次重复这个过程继续计算,例如![]() ,所以55263是“一刀两断”数.
,所以55263是“一刀两断”数.![]() ,所以3247不是“一刀两断”数.
,所以3247不是“一刀两断”数.
(1)判断5928是否为“一刀两断”数:_____(填是或否),并证明任意一个能被13整除的数是“一刀两断”数;
(2)对于一个“一刀两断”数![]() 均为正整数),规定
均为正整数),规定![]()
![]() .若
.若![]() 的千位数字满是
的千位数字满是![]() ,千位数字与十位数字相同,且能被65整除,求出所有满足条件的四位数
,千位数字与十位数字相同,且能被65整除,求出所有满足条件的四位数![]() 中,
中,![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
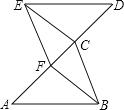
【题目】如图,已知A、F、C、D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE.
(1)求证:△ABC≌△DEF;
(2)若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
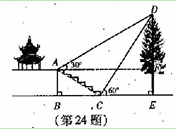
【题目】(本题7分)如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为![]() (即AB:BC=
(即AB:BC=![]() ),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
),且B、C、E三点在同一条盲线上。请根据以上杀件求出树DE的高度(测倾器的高度忽略不计).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com