
【题目】在平面直角坐标系xOy中,将点P沿着y轴翻折,得到的对应点再沿着直线l翻折得到点P1,则P1称为点P的“l变换点”.
(1)已知:点P(1,0),直线l:x=2,求点P的“l变换点”的坐标;
(2)若点Q和它的“l变换点”Q1的坐标分别为(2,1)和(3,2),求直线l的解析式;
(3)如图,⊙O的半径为2.
①若⊙O上存在点M,点M的“l变换点”M1在射线![]() x(x≥0)上,直线l:x=b,求b的取值范围;
x(x≥0)上,直线l:x=b,求b的取值范围;
②将⊙O在x轴上移动得到⊙E,若⊙E上存在点N,使得点N的“l变换点”N1在y轴上,且直线l的解析式为y=![]() x+1,求E点横坐标的取值范围.
x+1,求E点横坐标的取值范围.

【答案】(1)(5,0);(2)y=﹣5x+4;(3)①﹣1≤b≤2;②![]() ﹣4≤t≤
﹣4≤t≤![]() +4.
+4.
【解析】
(1)根据“l变换点”的定义,分别画出图形,即可解决问题;
(2)根据“l变换点”的定义,得到对称点的坐标,根据待定系数法即可得到结论;
(3)①根据“l变换点”的定义,画出图形,求出b的最大值以及最小值即可解决问题;
②如图6中,设点E关于y轴的对称点为E1,E1关于直线y=![]() x+1的对称点为E′,易知当点N在⊙E上运动时,点N′在⊙E′上运动,由此可见当⊙E′与y轴相切或相交时满足条件,想办法求出点E′的坐标即可解决问题.
x+1的对称点为E′,易知当点N在⊙E上运动时,点N′在⊙E′上运动,由此可见当⊙E′与y轴相切或相交时满足条件,想办法求出点E′的坐标即可解决问题.
解:(1)如图1,点P(1,0)关于y轴的对称点(﹣1,0),再关于直线x=2的对称点P1(5,0);
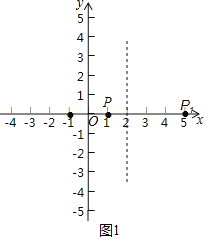
(2)点Q(2,1)关于y轴的对称点(﹣2,1),
设过点(﹣2,1)和(3,2)的直线的解析式为y=kx+b,
![]() ,
,
解得
k=﹣![]() ,b=
,b=![]() ,
,
∴y=﹣![]() x+
x+![]() ,
,
∵点(﹣2,1)和(3,2)关于直线l对称,
∴直线l过点(﹣2,1)和(3,2)连线的中点且与直线y=![]() x+
x+![]() 垂直,
垂直,
∵点(﹣2,1)和(3,2)连线的中点为(![]() ,
,![]() ),
),
∴设直线l的解析式为y=﹣5x+n,
∴![]() =﹣5×
=﹣5×![]() +n,
+n,
解得:n=4,
∴直线l的解析式为:y=﹣5x+4;
(3)①如图4中,
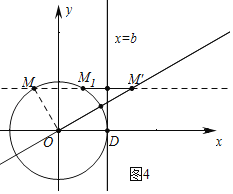
由题意b=![]() M1M′,由此可知,当M1M′的值最大时,可得b的最大值,
M1M′,由此可知,当M1M′的值最大时,可得b的最大值,
∵直线OM′的解析式为y=![]() x,
x,
∴tan∠M′OD=![]() ,
,
∴∠MM′O=∠M′OD=30°,
∵OM=2,易知,OM⊥OM′时,MM′的值最大,最大值为4,
∴b的最大值为2,
如图5中,易知当点M在x轴的正半轴上时,可得b的最小值,最小值为﹣1,
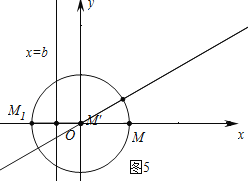
综上所述,满足条件的b取值范围为﹣1≤b≤2;
②设E(t,0),如图6中,设点E关于y轴的对称点为E1,E1关于直线y=![]() x+1的对称点为E′,易知当点N在⊙E上运动时,点N′在⊙E′上运动,由此可见当⊙E′与y轴相切或相交时满足条件.
x+1的对称点为E′,易知当点N在⊙E上运动时,点N′在⊙E′上运动,由此可见当⊙E′与y轴相切或相交时满足条件.
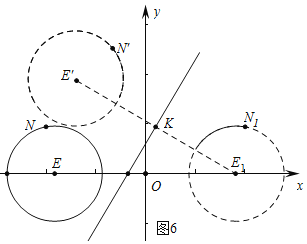
连接E1E′交直线y=![]() x+1于K,易知直线E1E′的解析式为y=﹣
x+1于K,易知直线E1E′的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
由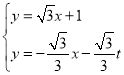 ,解得
,解得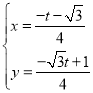 ,
,
∴K(![]() ,
,![]() ),
),
∵KE1=KE′,
∴E′(![]() ,
,![]() ),
),
当⊙E′与y轴相切时,|![]() |=2,解得t=
|=2,解得t=![]() ﹣4或
﹣4或![]() +4,
+4,
综上所述,满足条件的t的取值范围为![]() ﹣4≤t≤
﹣4≤t≤![]() +4.
+4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为_____.
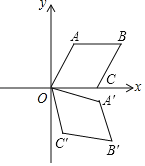
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与过点
,与过点![]() 平行于
平行于![]() 轴的直线相交于点
轴的直线相交于点![]() (点
(点![]() 在第一象限).抛物线的顶点
在第一象限).抛物线的顶点![]() 在直线
在直线![]() 上,对称轴与
上,对称轴与![]() 轴相交于点
轴相交于点![]() .平移抛物线,使其经过点
.平移抛物线,使其经过点![]() 、
、![]() ,则平移后的抛物线的解析式为__________.
,则平移后的抛物线的解析式为__________.
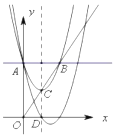
查看答案和解析>>
科目:初中数学 来源: 题型:
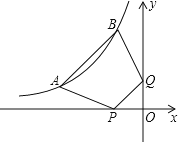
【题目】如图,点A(a,1),B(b,3)都在双曲线y=﹣![]() 上,点P,Q分别是x轴,y轴上的动点,则四边形ABPQ周长的最小值为( )
上,点P,Q分别是x轴,y轴上的动点,则四边形ABPQ周长的最小值为( )
A.4![]() B.6
B.6![]() C.2
C.2![]() +2
+2![]() D.8
D.8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
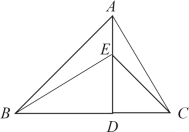
【题目】已知:如图,AD⊥BC,垂足为D,AD=BD,点E在AD上,∠CED=45°,
(1)请写出图中相等的线段: .(不包括已知条件中的相等线段)
(2)猜想BE与AC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)因式分解:![]() ___________.
___________.
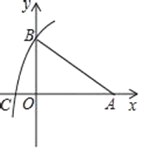
(2)如图,在平面直角坐标系中,A(6,0),B(0,2![]() ),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为_______.扇形BAC的面积为______.
),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为_______.扇形BAC的面积为______.
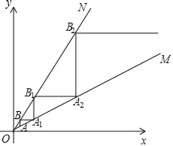
(3)在平面直角坐标系中,点![]() 在射线OM上,点
在射线OM上,点![]() 在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,则点B1的纵坐标为________,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_______.
在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,则点B1的纵坐标为________,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有红、黄两个布袋,红布袋中有两个完全相同的小球,分别标有数字2和4.黄布袋中有三个完全相同的小球,分别标有数字﹣2,﹣4和﹣6.小贤先从红布袋中随机取出一个小球,记录其标有的数字为x,再从黄布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点M的一个坐标为(x.y)
(1)用列表或画树状图的方法写出点M的所有可能坐标;
(2)求点M落在双曲线y=![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com