
如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线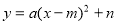 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为
的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为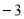 ,则点D的横坐标最大值为_______。
,则点D的横坐标最大值为_______。

8.
【解析】
试题分析:当C点横坐标最小时,抛物线顶点必为A(1,4),根据此时抛物线的对称轴,可判断出CD间的距离;当D点横坐标最大时,抛物线顶点为B(4,4),再根据此时抛物线的对称轴及CD的长,可判断出D点横坐标最大值.
试题解析:当点C横坐标为-3时,抛物线顶点为A(1,4),对称轴为x=1,此时D点横坐标为5,则CD=8;
当抛物线顶点为B(4,4)时,抛物线对称轴为x=4,且CD=8,故C(0,0),D(8,0);
由于此时D点横坐标最大,
故点D的横坐标最大值为8.
考点:二次函数的性质.
考点分析: 考点1:二次函数 定义: (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。  (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:  (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0);  (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0)  与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。  (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
一次函数y=ax+b的图象与反比例函数 的图象交于A,B两点,与
的图象交于A,B两点,与 轴交于点C.已知点A(-2,1),点B的坐标为(1,m).
轴交于点C.已知点A(-2,1),点B的坐标为(1,m).
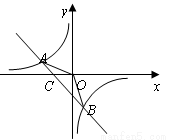
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积。
(3)根据图象写出使一次函数的值小于反比例函数的值的 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:填空题
反比例函数 与正比例函数
与正比例函数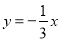 交于
交于 ,
, 两点,过点
两点,过点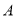 作
作 轴的平行线与过点
轴的平行线与过点 作
作 轴的平行线交于点C,则
轴的平行线交于点C,则 的面积为___________________.
的面积为___________________.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省西安市九年级下学期第一次月考数学试卷(解析版) 题型:选择题
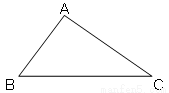
如图, 中,AC﹦5,
中,AC﹦5,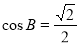 ,
, ,则
,则 的面积为( )
的面积为( )
A.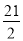 B.12 C. 14 D.21
B.12 C. 14 D.21
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(本题满分12分)在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.

(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市第一教研片九年级下学期第一次月考数学试卷(解析版) 题型:填空题
据统计,截至2014年底,全国的共产党员人数已超过80 300 000,这个数据用科学计数法可表示为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省九年级3月联考数学试卷(解析版) 题型:解答题
(本题8分)如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
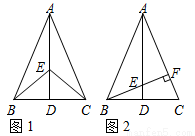
(1)求证:BE=CE;(4分)
(2)若BE的延长线交AC于点F,且BF⊥AC,垂足为F,如图2,∠BAC=45°,求证:△AEF≌△BCF.(4分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com