
【题目】已知:如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且∠B+∠D=180°,
求证:AE=AD+BE.

【答案】证明见解析.
【解析】
首先在AE上截取AM=AD,连接CM,再证明△AMC≌△ADC,可得∠3=∠D,再根据∠B+∠D=180°,∠3+∠4=180°,可以证出∠4=∠B,根据等角对等边可证出CM=BC,再根据等腰三角形的性质:等腰三角形底边上的高线与底边上的中线重合可得到ME-BE,再利用等量代换可证出AE=AD+BE.
证明:在AE上截取AM=AD,连接CM,

∵AC平分∠BAD,
∴∠1=∠2,
在△AMC和△ADC中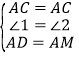 ,
,
∴△AMC≌△ADC(SAS),
∴∠3=∠D,
∵∠B+∠D=180°,∠3+∠4=180°,
∴∠4=∠B,
∴CM=CB,
∵CE⊥AB,
∴ME=EB(等腰三角形底边上的高线与底边上的中线重合),
∵AE=AM+ME,
∴AE=AD+BE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】观察如图所示的长方体.
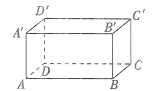
(1)用符号表示下列两棱的位置关系:AB___A′B′,AA′_____AB,D′A′_____D′C′,AD______BC.
(2) A′B′与BC所在的直线是两条不相交的直线,它们_____平行线.(填“是”或“不是”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海边的一段堤岸高出海平面12米,附近的某建筑物高出海平面50米,演习中的某潜水艇在海平面下30米处.
(1)现以海平面的高度为基准,将其记为0米,高于海平面记为正,低于海平面记为负,那么堤岸、附近建筑物及潜水艇的高度各应如何表示?
(2)若以堤岸高度为基准,则堤岸、建筑物及潜水艇的高度又应如何表示?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式:①a0=1;②a2a3=a5;③2﹣2=﹣ ![]() ;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2 , 其中正确的是( )
;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2 , 其中正确的是( )
A.①②③
B.①③⑤
C.②③④
D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是( ) 
A.80°
B.110°
C.120°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为 . 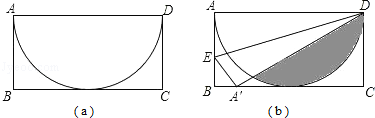
查看答案和解析>>
科目:初中数学 来源: 题型:
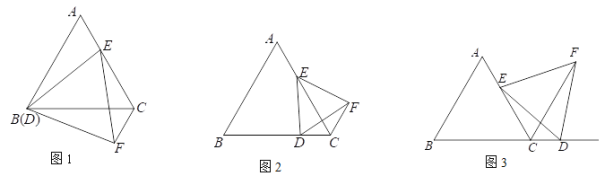
【题目】△ABC是等边三角形,点E在AC边上,点D是BC边上的一个动点,以DE为边作等边△DEF,连接CF.
(1)如图1,当点D与点B重合时,求证:△ADE≌△CDF;
(2)如图2,当点D运动到如图2的位置时,猜想CE、CF、CD之间的数量关系,并说明理由;
(3)如图3,当点D在BC延长线上时,直接写出CE、CF、CD之间的数量关系,不证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想三角形外心的概念,我们可引入如下概念. 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
(1)应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= ![]() AB,求∠APB的度数.
AB,求∠APB的度数. 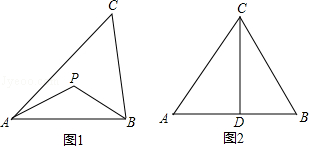
(2)探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上的点A,B对应的数分别是x,y,且|x+100|+(y﹣200)2=0,点P为数轴上从原点出发的一个动点,速度为30单位长度/秒.
(1)求点A,B两点之间的距离;
(2)若点A向右运动,速度为10单位长度/秒,点B向左运动,速度为20单位长度/秒,点A,B和P三点同时开始运动,点P先向右运动,遇到点B后立即掉后向左运动,遇到点A再立即掉头向右运动,如此往返,当A,B两点相距30个单位长度时,点P立即停止运动,求此时点P移动的路程为多少个单位长度?
(3)若点A,B,P三个点都向右运动,点A,B的速度分别为10单位长度/秒,20单位长度/秒,点M、N分别是AP、OB的中点,设运动的时间为t(0<t<10),在运动过程中①![]() 的值不变;②
的值不变;②![]() 的值不变,可以证明,只有一个结论是正确的,请你找出正确的结论并求值.
的值不变,可以证明,只有一个结论是正确的,请你找出正确的结论并求值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com