
【题目】联想三角形外心的概念,我们可引入如下概念. 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
(1)应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= ![]() AB,求∠APB的度数.
AB,求∠APB的度数. 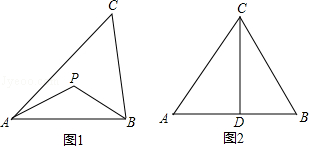
(2)探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
【答案】
(1)解:①若PB=PC,连接PB,则∠PCB=∠PBC,
∵CD为等边三角形的高,
∴AD=BD,∠PCB=30°,
∴∠PBD=∠PBC=30°,
∴PD= ![]() DB=
DB= ![]() AB,
AB,
与已知PD= ![]() AB矛盾,∴PB≠PC,
AB矛盾,∴PB≠PC,
②若PA=PC,连接PA,同理可得PA≠PC,
③若PA=PB,由PD= ![]() AB,得PD=BD,
AB,得PD=BD,
∴∠APD=45°,
故∠APB=90°
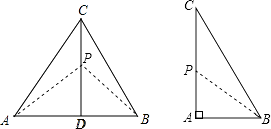
(2)解:∵BC=5,AB=3,
∴AC= ![]() =
= ![]() =4,
=4,
①若PB=PC,设PA=x,则x2+32=(4﹣x)2,
∴x= ![]() ,即PA=
,即PA= ![]() ,
,
②若PA=PC,则PA=2,
③若PA=PB,由图知,在Rt△PAB中,不可能.
故PA=2或 ![]() .
.
【解析】应用:连接PA、PB,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况利用等边三角形的性质求出PD与AB的关系,然后判断出只有情况③是合适的,再根据等腰直角三角形的性质求出∠APB=45°,然后即可求出∠APB的度数; 探究:先根据勾股定理求出AC的长度,根据准外心的定义,分①PB=PC,②PA=PC,③PA=PB三种情况,根据三角形的性质计算即可得解.
【考点精析】掌握线段垂直平分线的性质和等腰三角形的性质是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;等腰三角形的两个底角相等(简称:等边对等角).


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于点A(2,0)和点B,与y轴交于点C,顶点为点D,对称轴为直线x=﹣1,点E为线段AC的中点,点F为x轴上一动点.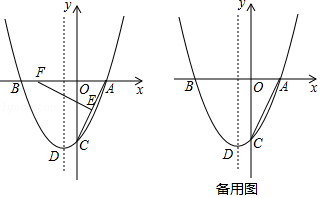
(1)直接写出点B的坐标,并求出抛物线的函数关系式;
(2)当点F的横坐标为﹣3时,线段EF上存在点H,使△CDH的周长最小,请求出点H,使△CDH的周长最小,请求出点H的坐标;
(3)在y轴左侧的抛物线上是否存在点P,使以P,F,C,D为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线l1:y=2x+1
(1)若将直线l1平移,使之经过点(1,-5),求平移后直线的解析式;
(2)若直线l2:y=x+m与直线l1的交点在第二象限,求m的取值范围;
(3)如图,直线y=x+b与直线y=nx+2n(n≠0)的交点的横坐标为-5,求关于x的不等式组0<nx+2n<x+b的解集.
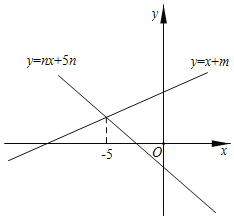
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内有三点A(2,2![]() ),B(5,2
),B(5,2![]() ),C(5,
),C(5,![]() )
)
(1)请确定一个点D,使四边形ABCD为长方形,写出点D的坐.
(2)求这个四边形的面积(精确到0.01).
(3)将这个四边形向右平移2个单位,再向下平移![]() 个单位,求平移后四个顶点的坐标.
个单位,求平移后四个顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ ![]() .其中正确的个数为( )
.其中正确的个数为( ) 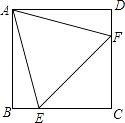
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在一次广播操比赛中,初二 (1)班、初二(2)班、初二(3)班的各项得分如下:
服装统一 | 动作整齐 | 动作准确 | |
初二(1)班 |
|
|
|
初二(2)班 |
|
|
|
初二(3)班 |
|
|
|
(1)填空:根据表中提供的信息,在服装统一方面,三个班得分的平均数是________;在动作整齐方面三个班得分的众数是________;在动作准确方面最有优势的是________班.
(2)如果服装统一、动作整齐、动作准确三个方面的重要性之比为![]() ,那么这三个班的排名顺序怎样?为什么?
,那么这三个班的排名顺序怎样?为什么?
(3)在(2)的条件下,你对三个班级中排名最靠后的班级有何建议?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了增强学生体质,全面实施“学生饮用奶”营养工程.某品牌牛奶供应商提供了原味、草莓味、菠萝味、香橙味、核桃味五种口味的牛奶提供学生饮用.浠马中学为了了解学生对不同口味牛奶的喜好,对全校订购牛奶的学生进行了随机调查(每盒各种口味牛奶的体积相同),绘制了如图两张不完整的人数统计图: 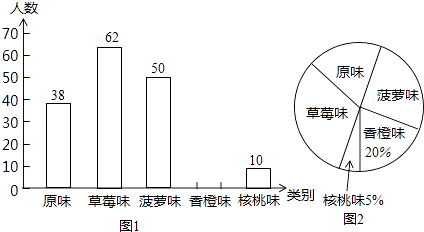
(1)本次被调查的学生有名;
(2)补全上面的条形统计图1,并计算出喜好“菠萝味”牛奶的学生人数在扇形统计图中所占圆心角的度数;
(3)该校共有1200名学生订购了该品牌的牛奶,牛奶供应商每天只为每名订购牛奶的学生配送一盒牛奶.要使学生每天都喝到自己喜好的口味的牛奶,牛奶供应商每天送往该校的牛奶中,草莓味要比原味多送多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业1~5月份利润的变化情况图所示,以下说法与图中反映的信息相符的是( )
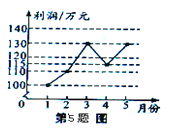
A. 1~2月份利润的增长快于2~3月份分利润的增长
B. 1~4月份利润的极差与1~5月份利润的极差不同
C. 1~5月份利润的的众数是130万元
D. 1~5月份利润的中位数为120万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com