
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于点A(2,0)和点B,与y轴交于点C,顶点为点D,对称轴为直线x=﹣1,点E为线段AC的中点,点F为x轴上一动点.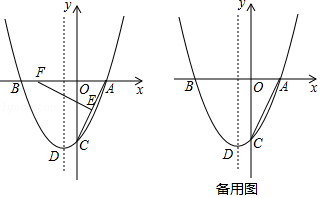
(1)直接写出点B的坐标,并求出抛物线的函数关系式;
(2)当点F的横坐标为﹣3时,线段EF上存在点H,使△CDH的周长最小,请求出点H,使△CDH的周长最小,请求出点H的坐标;
(3)在y轴左侧的抛物线上是否存在点P,使以P,F,C,D为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:由A、B关于x=﹣1对称,得
B(﹣4,0),
∵抛物线y=ax2+bx﹣4过A(2,0)、B(﹣4,0),
∴ ![]() ,
,
解得: ![]() ,
,
∴y= ![]() x2+x﹣4
x2+x﹣4
(2)
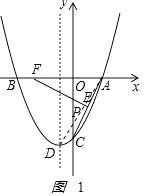
解:如图1,
当x=0时,y=﹣4,即C(0,﹣4),
y= ![]() x2+x﹣4=
x2+x﹣4= ![]() (x+1)2﹣
(x+1)2﹣ ![]()
∴D(﹣1,﹣ ![]() ),
),
∵E为线段AC的中点,A(2,0),C(0,﹣4),
∴E(1,﹣2).
∵点F横坐标为﹣3,
∴F(﹣3,0),
∴AF=5,CF= ![]() =
= ![]() =5,
=5,
∴AF=CF,
∵E为线段AC的中点,
∴EF垂直平分AC,
∴A、C关于直线EF轴对称,连接AD,与直线EF交点即为所求H,
∴EF⊥AC.
设直线EF关系式为y=k1x+b1,
∴ ![]() ,
,
解得:  ,
,
∴直线EF:y=﹣ ![]() x﹣
x﹣ ![]() ,
,
设直线AD关系式为y=k2x+b2,
∴ 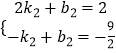 ,
,
解得:  ,
,
∴y= ![]() x﹣3,
x﹣3,
联立AD,EF,得 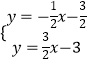 ,
,
∴ 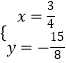 ,
,
∴H( ![]() ,﹣
,﹣ ![]() )
)
(3)
解:若CD为对角线,不存在;
若CD为边,则PF∥CD且PF=CD,
∵C(0,﹣4),D(﹣1,﹣ ![]() ),点F为x轴上一动点,
),点F为x轴上一动点,
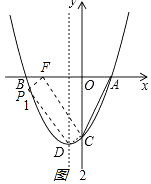
如图2,PDCF是平行四边形,对角线的纵坐标为﹣ ![]() ,P点纵坐标﹣
,P点纵坐标﹣ ![]() ,
,
当y=﹣ ![]() 时,
时, ![]() x2+x﹣4=﹣
x2+x﹣4=﹣ ![]() ,解得x1=﹣1+2
,解得x1=﹣1+2 ![]() (舍),x2=﹣1﹣2
(舍),x2=﹣1﹣2 ![]() ,
,
∴P1(﹣1﹣2 ![]() ,﹣
,﹣ ![]() ).
).
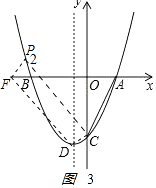
如图3,PFDC是平行四边形,对角线的交点坐标为﹣2,P点坐标为 ![]() ,
,
当y= ![]() 时,
时, ![]() x2+x﹣4=
x2+x﹣4= ![]() ,解得x1=﹣1+
,解得x1=﹣1+ ![]() (舍),x2=﹣1﹣
(舍),x2=﹣1﹣ ![]() ,
,
∴P2(﹣1﹣ ![]() ,
, ![]() ).
).
综上所述:在y轴左侧的抛物线上存在点P,使以P,F,C,D为顶点的四边形是平行四边形,点P的坐标(﹣1﹣2 ![]() ,﹣
,﹣ ![]() ),(﹣1﹣
),(﹣1﹣ ![]() ,
, ![]() )
)
【解析】(1)根据轴对称,可得B点坐标,根据待定系数法,可得答案;(2)根据自变量与函数值的对应关系,可得C点坐标,根据配方法,可得D点坐标,根据勾股定理,可得CF的长,根据等腰三角形的性质,可得A,C关于EF对称,根据轴对称的性质,可得PA=PC,根据两点之间线段最短,可得P是AD与EF的交点,根据解方程组,可得答案;(3)根据平行四边形的对角线互相平分,可得P点的纵坐标,根据自变量与函数值的对应关系,可得答案.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对平行四边形的性质的理解,了解平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( ) 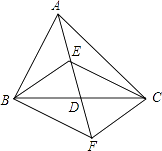
A.BE⊥CE
B.BF∥CE
C.BE=CF
D.AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图所示的长方体.
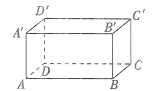
(1)用符号表示下列两棱的位置关系:AB___A′B′,AA′_____AB,D′A′_____D′C′,AD______BC.
(2) A′B′与BC所在的直线是两条不相交的直线,它们_____平行线.(填“是”或“不是”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如下表和图①:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
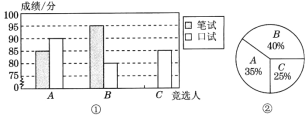
(1)请将表格和图①中的空缺部分补充完整;
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图②(没有弃权票,每名学生只能推荐一人),请计算每人的得票数;
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4∶3∶3的比确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D为直线BC上一动点(点D不与B、C重合)以AD为边作正方形ADEF,使∠DAF=∠BAC,连接CF.
(1)如图1,当点D在线段BC上时,求证:BD=CF;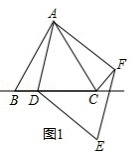
(2)如图2,当点D在线段BC的延长线上,且∠BAC=90°时.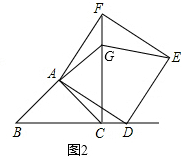
①问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
②延长BA交CF于点G,连接GE,若AB=2 ![]() ,CD=BC,请求出GE的长.
,CD=BC,请求出GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海边的一段堤岸高出海平面12米,附近的某建筑物高出海平面50米,演习中的某潜水艇在海平面下30米处.
(1)现以海平面的高度为基准,将其记为0米,高于海平面记为正,低于海平面记为负,那么堤岸、附近建筑物及潜水艇的高度各应如何表示?
(2)若以堤岸高度为基准,则堤岸、建筑物及潜水艇的高度又应如何表示?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式:①a0=1;②a2a3=a5;③2﹣2=﹣ ![]() ;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2 , 其中正确的是( )
;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2 , 其中正确的是( )
A.①②③
B.①③⑤
C.②③④
D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想三角形外心的概念,我们可引入如下概念. 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
(1)应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= ![]() AB,求∠APB的度数.
AB,求∠APB的度数. 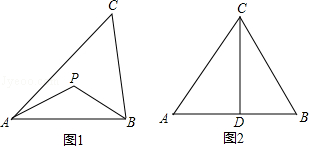
(2)探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com