
【题目】平面内有三点A(2,2![]() ),B(5,2
),B(5,2![]() ),C(5,
),C(5,![]() )
)
(1)请确定一个点D,使四边形ABCD为长方形,写出点D的坐.
(2)求这个四边形的面积(精确到0.01).
(3)将这个四边形向右平移2个单位,再向下平移![]() 个单位,求平移后四个顶点的坐标.
个单位,求平移后四个顶点的坐标.
【答案】(1)D(2,![]() );(2)s≈4.24;(3) A'(4,-
);(2)s≈4.24;(3) A'(4,-![]() )B'(7,-
)B'(7,-![]() )C'(7,-2
)C'(7,-2![]() ) D'(4,-2
) D'(4,-2![]() ).
).
【解析】
(1)抓住矩形的特点,即对边平行,邻边互相垂直的性质,AB∥DC,AB⊥AD,BC∥AD,BC⊥DC及平行线的性质,第三条直线与平行线中的任何一条平行,那么,它与另一条也平行.
(2)根据两点间的距离公式求出边长,再根据矩形的面积公式求出面积.
(3)根据平移及点的移动规律即可得解.
(1)由题意知,四边形ABCD是矩形,如图,
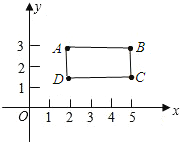
∴AB∥DC,
又∵AB平行于x轴(由AB两点的坐标可知),
∴DC也平行于x轴(平行线的性质),
∵AB⊥AD,
∴AD垂直于x轴.
∴D点既在经过C(5,![]() )平行于x轴的平行线DC上,又在经过A(2,2
)平行于x轴的平行线DC上,又在经过A(2,2![]() )的x轴的垂线AD上,
)的x轴的垂线AD上,
∴D(2,![]() );
);
(2)由题意可知:AB=5-2=3,
AD=![]() ,
,
故四边形ABCD的面积是AB×AD=3![]() ≈4.24;
≈4.24;
(3)∵四边形ABCD向右平移2个单位,再向下平移3![]() 个单位,
个单位,
∴A(2+2,2![]() -3
-3![]() ),B(5+2,2
),B(5+2,2![]() -3
-3![]() ),C(5+2,
),C(5+2,![]() -3
-3![]() ),D(2+2,
),D(2+2,![]() -3
-3![]() ),
),
即A(4,-![]() ),B(7,-
),B(7,-![]() ),C(7,-2
),C(7,-2![]() ),D(4,-2
),D(4,-2![]() ).
).


科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D为直线BC上一动点(点D不与B、C重合)以AD为边作正方形ADEF,使∠DAF=∠BAC,连接CF.
(1)如图1,当点D在线段BC上时,求证:BD=CF;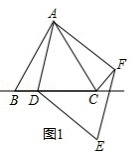
(2)如图2,当点D在线段BC的延长线上,且∠BAC=90°时.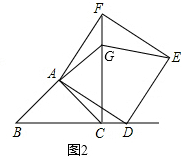
①问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
②延长BA交CF于点G,连接GE,若AB=2 ![]() ,CD=BC,请求出GE的长.
,CD=BC,请求出GE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,A、B是切点,点C是劣弧AB上的一个动点,若∠P=40°,则∠ACB的度数是( ) 
A.80°
B.110°
C.120°
D.140°
查看答案和解析>>
科目:初中数学 来源: 题型:
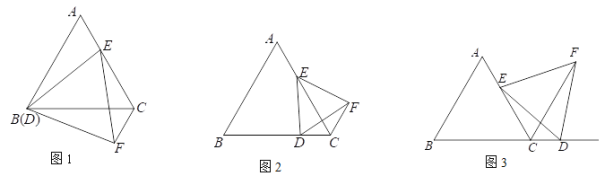
【题目】△ABC是等边三角形,点E在AC边上,点D是BC边上的一个动点,以DE为边作等边△DEF,连接CF.
(1)如图1,当点D与点B重合时,求证:△ADE≌△CDF;
(2)如图2,当点D运动到如图2的位置时,猜想CE、CF、CD之间的数量关系,并说明理由;
(3)如图3,当点D在BC延长线上时,直接写出CE、CF、CD之间的数量关系,不证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们不妨将横坐标、纵坐标均为整数的点称之为“湘一点”.
(1)求函数y=![]() x-3的图象上所有“湘一点”的坐标;
x-3的图象上所有“湘一点”的坐标;
(2)若直线y=mx+m(m为常数)与直线y=x-2的交点为“湘一点”,试求出整数m的值.
(3)若直线y=-x+b、直线y=3、直线y=x+2所围成的平面图形中(不含边界)共有6个“湘一点”,试求出常数b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】联想三角形外心的概念,我们可引入如下概念. 定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图1,若PA=PB,则点P为△ABC的准外心.
(1)应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD= ![]() AB,求∠APB的度数.
AB,求∠APB的度数. 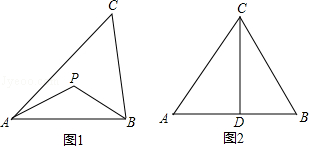
(2)探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:
(1)求出足球和篮球的单价;
(2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?
(3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com