
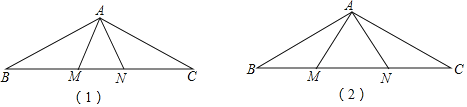
【题目】已知如图,M、N是△ABC的BC边上两点,且AB=AC,BM=CN
(1)如图1,证明:△ABN≌△ACM;
(2)如图2,当∠ANB=2∠B时,直接写出图中所有等腰三角形(△ABC除外)
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】一个两位数,个位数比十位数大2,若把各位数字和十位数字对调,则所得的新的两位数比原数的两倍少17.若设原数的个位数为![]() ,十位数字为
,十位数字为![]() ,则下列方程组正确的是( )
,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为6 m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是

A. AB=12 m B. MN∥AB
C. △CMN∽△CAB D. CM∶MA=1∶2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为8的等边三角形ABC中,点D沿射线AB方向由A向B运动,点F同时从C出发,以相同的速度每秒1个单位长度沿射线BC方向运动,过点D作DE⊥AC,连结DF交射线AC于点G.
(1)当DF⊥AB时,求AD的长;
(2)求证:EG=![]() AC.
AC.
(3)点D从A出发,经过几秒,CG=1.6?直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.

(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为3万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.4万元,设可变成本平均每年增长的百分率为x.
(1)用含x的代数式表示第3年的可变成本为万元.
(2)如果该养殖户第3年的养殖成本为6.456万元,求可变成本平均每年增长的百分率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com