
【题目】如图,AE平分∠BAC,BD=DC,DE⊥BC,EM⊥AB.若AB=9,AC=5,则AM的长为______.

【答案】7
【解析】
过点E作EN⊥AC的延长线于点N,连接BE、EC,利用角平分线的性质、垂直平分线的性质得到EM=EN,EB=EC,证明Rt△BME≌Rt△CNE(HL),得到BM=CN,证明Rt△AME≌Rt△ANE(HL),得到AM=AN,由AM=AB-BM=AB-CN=AB-(AN-AC)=AB-AN+AC=AB-AM+AC,即AM=9-AM+5,即可解答.
解:如图,过点E作EN⊥AC的延长线于点N,连接BE、EC,
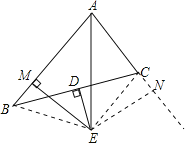
∵BD=DC,DE⊥BC
∵BE=EC.
∵AE平分∠BAC,EM⊥AB,EN⊥AC,
∴EM=EN,∠EMB=∠ENC=90°.
在Rt△BME和Rt△CNE中,
![]() ,
,
∴Rt△BME≌Rt△CNE(HL)
∴BM=CN,
在RtAME和Rt△ANE中,
![]() ,
,
∴Rt△AME≌Rt△ANE(HL)
∴AM=AN,
∴AM=AB-BM=AB-CN=AB-(AN-AC)=AB-AN+AC=AB-AM+AC,
即AM=9-AM+5
2AM=9+5
2AM=14
AM=7.
故答案为:7.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y= ![]() +bx+c的图象如图所示,对称轴为直线x=1.有位学生写出了以下五个结论:①ac>0;②方程ax2+bx+c=0的两根是
+bx+c的图象如图所示,对称轴为直线x=1.有位学生写出了以下五个结论:①ac>0;②方程ax2+bx+c=0的两根是 ![]() =﹣1,
=﹣1, ![]() =3;③2a﹣b=0;④当x>1时,y随x的增大而减小;则以上结论中正确的有( ).
=3;③2a﹣b=0;④当x>1时,y随x的增大而减小;则以上结论中正确的有( ).
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在矩形ABCD中,BC=8,CD=6,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则△BDE的面积为( )

A. ![]() B.
B. ![]() C. 21D. 24
C. 21D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往海滨公园. 如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是____,因变量是______;
(2)小明家到滨海公园的路程为____ km,小明在中心书城逗留的时间为____ h;
(3)小明出发______小时后爸爸驾车出发;
(4)图中A点表示___________________________________;
(5)小明从中心书城到滨海公园的平均速度为______km/h,小明爸爸驾车的平均速度为______km/h;(补充;爸爸驾车经过______追上小明);
(6)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )
A.2 ![]()
B.2 ![]()
C.2 ![]()
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
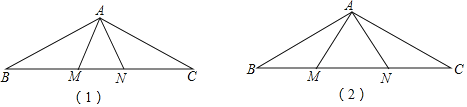
【题目】已知如图,M、N是△ABC的BC边上两点,且AB=AC,BM=CN
(1)如图1,证明:△ABN≌△ACM;
(2)如图2,当∠ANB=2∠B时,直接写出图中所有等腰三角形(△ABC除外)
查看答案和解析>>
科目:初中数学 来源: 题型:
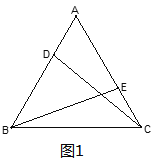
【题目】在等边△ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以每分钟1米的速度由A向B和由C向A爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、E处,请问:
(1)如图1,在爬行过程中,CD和BE始终相等吗,请证明?
(2)如果将原题中的“由A向B和由C向A爬行”,改为“沿着AB和CA的延长线爬行”,EB与CD交于点Q,其他条件不变,蜗牛爬行过程中∠CQE的大小保持不变,请利用图2说明:∠CQE=60°;
(3)如果将原题中“由C向A爬行”改为“沿着BC的延长线爬行,连接DE交AC于F”,其他条件不变,如图3,则爬行过程中,证明:DF=EF


![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
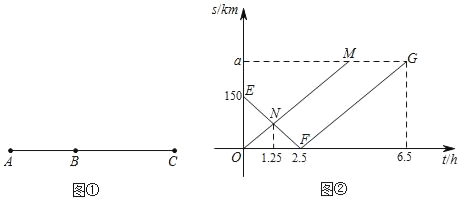
【题目】如图①,A、B、C三地依次在一直线上,两辆汽车甲、乙分别从A、B两地同时出发驶向C地,如图②,是两辆汽车行驶过程中到C地的距离s(km)与行驶时间t(h)的关系图象,其中折线段EF﹣FG是甲车的图象,线段OM是乙车的图象.
(1)图②中,a的值为 ;点M的坐标为 ;
(2)当甲车在乙车与B地的中点位置时,求行驶的时间t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com