
【题目】如图,学校准备新建一个长度为L的读书长廊,并准备用若干块带有花纹和没有花纹的两种规格大小相同的正方形地面砖搭配在一起,按图中所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.3m.

(1)按图示规律,第一图案的长度L1= ;第二个图案的长度L2= ;
(2)请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln(m)之间的关系;
(2)当走廊的长度L为30.3m时,请计算出所需带有花纹图案的瓷砖的块数.
【答案】(1)0.9,1.5;(2)L=(2n+1)×0.3;(3)需要50个有花纹的图案.
【解析】
试题分析:(1)观察题目中的已知图形,可得前两个图案中有花纹的地面砖分别有:1,2个,第二个图案比第一个图案多1个有花纹的地面砖,所以可得第n个图案有花纹的地面砖有n块;第一个图案边长3×0.3=L,第二个图案边长5×0.3=L,
(2)由(1)得出则第n个图案边长为L=(2n+1)×0.3;
(3)根据(2)中的代数式,把L为30.3m代入求出n的值即可.
解:(1)第一图案的长度L1=0.3×3=0.9,第二个图案的长度L2=0.3×5=1.5;
故答案为:0.9,1.5;
(2)观察可得:第1个图案中有花纹的地面砖有1块,第2个图案中有花纹的地面砖有2块,…
故第n个图案中有花纹的地面砖有n块;
第一个图案边长L=3×0.3,第二个图案边长L=5×0.3,则第n个图案边长为L=(2n+1)×0.3;
(3)把L=30.3代入L=(2n+1)×0.3中得:
30.3=(2n+1)×0.3,
解得:n=50,
答:需要50个有花纹的图案.


科目:初中数学 来源: 题型:
【题目】如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
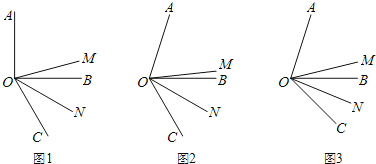
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距450千米,一辆快车和一辆慢车上午7点分别从甲、乙两地以不变的速度同时出发开往乙地和甲地,快车到达乙地后休息一个小时按原速返回,快车返回甲地时已是下午5点,慢车在快车前一个小时到达甲地.试根据以上信息解答以下问题:
(1)分别求出快车、慢车的速度(单位:千米/小时);
(2)从两车出发直至慢车达到甲地的过程中,经过几小时两车相距150千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,CB=3,点D是BC边上的点,将△ADC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
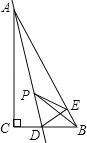
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠A=30°,∠B=60°

(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)连接DE,则∠ADE= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转,如图2,设旋转时间为t(0秒≤t≤90秒).
(1)用含t的代数式表示∠MOA的度数.
(2)在运动过程中,当∠AOB第二次达到60°时,求t的值.
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com