
【题目】甲、乙两地相距450千米,一辆快车和一辆慢车上午7点分别从甲、乙两地以不变的速度同时出发开往乙地和甲地,快车到达乙地后休息一个小时按原速返回,快车返回甲地时已是下午5点,慢车在快车前一个小时到达甲地.试根据以上信息解答以下问题:
(1)分别求出快车、慢车的速度(单位:千米/小时);
(2)从两车出发直至慢车达到甲地的过程中,经过几小时两车相距150千米.
【答案】(1)求出快车、慢车的速度分别是100千米/小时,50千米/小时;(2)从两车出发直至慢车达到甲地的过程中,经过2小时或4小时、8小时两车相距150千米.
【解析】
试题分析:(1)根据速度=![]() 直接列算式计算即可;
直接列算式计算即可;
(2)设经过x个小时,分三种情形讨论①相遇前两车相距150千米②相遇后且快车未到达甲地时两车相距150千米(或恰好到达但尚未休息)③休息后快车从乙地出发在慢车后追至相距150千米,根据速度×时间=路程,列出方程,求出x的值即可.
解:(1)根据题意得:
v快=450÷4.5=100千米/小时,
v慢=450÷9=50千米/小时;
答:求出快车、慢车的速度分别是100千米/小时,50千米/小时;
(2)设经过x个小时两车相距150千米,分三种情形讨论:
①相遇前两车相距150千米:(100+50)x+150=450,解得x=2;
②相遇后且快车未到达甲地时两车相距150千米(或恰好到达但尚未休息):(100+50)x﹣150=450,解得x=4;
③休息后快车从乙地出发在慢车后追至相距150千米:100(x﹣5.5)+150=50x,解得x=8;
答:从两车出发直至慢车达到甲地的过程中,经过2小时或4小时、8小时两车相距150千米.


科目:初中数学 来源: 题型:
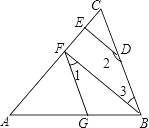
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°.

(1)在BC边上作一点P,使得点P到点C的距离与点P到边AB的距离相等(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=8,BC=6,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,学校准备新建一个长度为L的读书长廊,并准备用若干块带有花纹和没有花纹的两种规格大小相同的正方形地面砖搭配在一起,按图中所示的规律拼成图案铺满长廊,已知每个小正方形地面砖的边长均为0.3m.

(1)按图示规律,第一图案的长度L1= ;第二个图案的长度L2= ;
(2)请用代数式表示带有花纹的地面砖块数n与走廊的长度Ln(m)之间的关系;
(2)当走廊的长度L为30.3m时,请计算出所需带有花纹图案的瓷砖的块数.
查看答案和解析>>
科目:初中数学 来源: 题型:
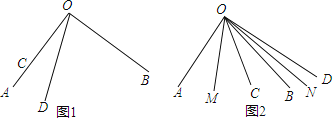
【题目】已知∠AOB=90°,∠COD=30°.
(1)如图1,当点O、A、C在同一条直线上时,∠BOD的度数是 ;
(2)将∠COD从图1的位置开始,绕点O逆时针方向旋转n°(即∠AOC=n°),且0<n<180.
①如果∠COD的一边与∠AOB的一边垂直,则n= .
②当60<n<90时(如图2),作射线OM平分∠AOC,射线ON平分∠BOD,试求∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1cm的若干个正方形叠加行成的图形,其中第一个图形由1个正方形组成,周长为4cm,第二个图形由4个正方形组成,周长为10cm.第三个图形由9个正方形组成,周长为16cm,依次规律…
(1)第四个图形有 个正方形组成,周长为 cm.
(2)第n个图形有 个正方形组成,周长为 cm.
(3)若某图形的周长为58cm,计算该图形由多少个正方形叠加形成.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题,
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴m=﹣3,n=3
问题(1)若x2+2y2﹣2xy+4y+4=0,求xy的值.
(2)已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com