
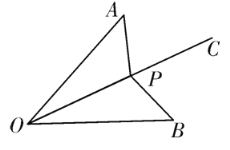
【题目】如图,已知射线OC为∠AOB的平分线,且OA=OB,点P是射线OC上的任意一点,连接AP、BP.
(1)求证:△AOP≌△BOP;
(2)若∠AOB=50°,且点P是△AOB的外心,求∠APB的度数;
(3)若∠AOB=50°,且△OAP为钝角三角形,直接写出∠OAP的取值范围.
【答案】(1)证明见解析;(2)∠APB=100°;(3)0°<∠OAP< 65°或90°<∠OAP<155°.
【解析】
(1)根据“SAS”证明即可;
(2)根据三角形外心定义得到PA=PB=PO,根据等腰三角形性质和三角形的外角性质求出∠APC=50°,根据∠APO=∠BPO即可求解;
(3)根据题意得![]() ,分
,分![]() 为钝角和
为钝角和![]() 为钝角两种情况讨论即可.
为钝角两种情况讨论即可.
解:(1)∵OP平分∠AOB,
∴∠AOP=∠BOP,
又∵OA=OB,OP=OP,
∴△AOP≌△BOP;
(2)∵∠AOB=50°,
∴∠AOP=∠BOP=25°,
∵点P是△AOB的外心,
∴PA=PB=PO,
∴∠A=∠AOP=25°,
∴∠APC=∠A+∠AOP=50°,
∵△AOP≌△BOP,
∴∠APO=∠BPO,
∴∠BPC=∠APC=50°,
∴∠APB=100°;
(3)∵∠AOB=50°,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
如图1,当![]() 为钝角时,
为钝角时,
90°<∠OAP<155° ;
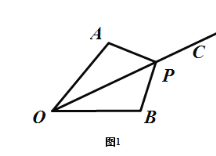
如图2,当![]() 为钝角时,
为钝角时,
90°<∠OPA<155°,
即90°<![]() <155°,
<155°,
∴0°<∠OAP< 65°

∴∠OAP的取值范围为:90°<∠OAP<155°或0°<∠OAP< 65°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
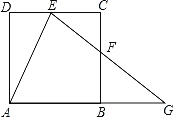
【题目】如图,在正方形ABCD中,点E在DC边上(不与点C,点D重合),点G在AB的延长线上,连结EG,交边BC于点F,且EG=AG,连结AE,AF,设∠AED=![]() ,∠GFB=
,∠GFB=![]() .
.
(1)求![]() ,
,![]() 之间等量关系;
之间等量关系;
(2)若△ADE≌△ABF,AB=2,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
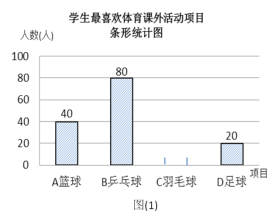
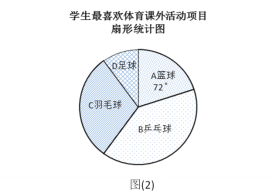
【题目】某学校为了丰富学生课余生活,决定开设以下体育课外活动项目:A篮球;B乒乓球;C羽毛球;D足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有__________人;
(2)请你将条形统计图(1)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行钢笔书法大赛,对各年级同学的获奖情况进行了统计,并绘制了如下两幅不完整的统计图.
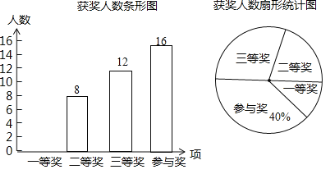
请结合图中相关信息解答下列问题:
(1)扇形统计图中三等奖所在扇形的圆心角的度数是______度;
(2)请将条形统计图补全;
(3)获得一等奖的同学中有![]() 来自七年级,有
来自七年级,有![]() 来自九年级,其他同学均来自八年级.现准备从获得一等奖的同学中任选2人参加市级钢笔书法大赛,请通过列表或画树状图的方法求所选出的2人中既有八年级同学又有九年级同学的概率.
来自九年级,其他同学均来自八年级.现准备从获得一等奖的同学中任选2人参加市级钢笔书法大赛,请通过列表或画树状图的方法求所选出的2人中既有八年级同学又有九年级同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为反比例函数y=![]() 在第一象限上的两点,AC⊥y轴于点C,BD⊥x轴于点D,若B点的横坐标是A点横坐标的一半,且图中阴影部分的面积为k﹣2,则k的值为( )
在第一象限上的两点,AC⊥y轴于点C,BD⊥x轴于点D,若B点的横坐标是A点横坐标的一半,且图中阴影部分的面积为k﹣2,则k的值为( )
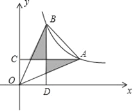
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
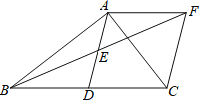
【题目】如图,在![]() ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:![]() AEF≌△DEB;
AEF≌△DEB;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=4![]() ,∠CAB=30°,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为_____.
,∠CAB=30°,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为_____.
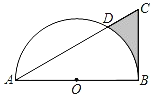
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】港口 A、B、C 依次在同一条直线上,甲、乙两艘船同时分别从 A、B两港出发,匀速驶向 C 港,甲、乙两船与 B 港的距离 y(海里)与行驶时间 x 时)之间的函数关系如图所示,则下列说法错误的是( )
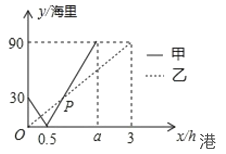
A.甲船平均速度为 60 海里/时B.乙船平均速度为 30 海里/时
C.甲、乙两船在途中相遇两次D.A、C 两港之间的距离为 120 海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是边
是边![]() 上的一点(不与点
上的一点(不与点![]() 重合),边
重合),边![]() 上点
上点![]() 在点
在点![]() 的右边且
的右边且![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,连接
,连接![]() .
.
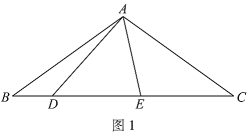
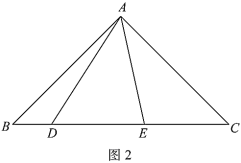
(1)如图1,
①依题意补全图1;
②求证:![]() ;
;
(2)如图2,![]() ,用等式表示线段
,用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com