【题目】如图，把
放置在量角器上，
与量角器的中心重合，读得射线
、
分别经过刻度
和
，把绕点逆时针方向旋转到
，下列结论：
①
；
②若射线
经过刻度
，则
与
互补；
③若
，则射线经过刻度45．
其中正确的是（ ）
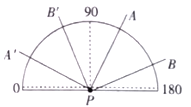
A.①②B.①③C.②③D.①②③
计算高手系列答案科目：初中数学 来源： 题型：
【题目】综合与实践
问题情境
在数学活动课上，老师和同学们以“线段与角的共性”为主题开展数学活动．发现线段的中点的概念与角的平分线的概念类似，甚至它们在计算的方法上也有类似之处，它们之间的题目可以转换，解法可以互相借鉴．如图1，点
是线段
上的一点，
是
的中点，
是
的中点．
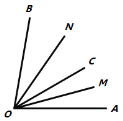
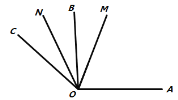
图1 图2 图3
（1）问题探究
①若
，
，求
的长度；（写出计算过程）
②若
，
，则
___________；（直接写出结果）
（2）继续探究
“创新”小组的同学类比想到：如图2，已知
，在角的内部作射线
，再分别作
和
的角平分线
，
．
③若
，求
的度数；（写出计算过程）
④若
，则
_____________![](http://thumb.zyjl.cn/questionBank/Upload/2020/11/27/14/ed63c8b7/SYS202011271400221063772281_ST/SYS202011271400221063772281_ST.026.png"){kind=small}
；（直接写出结果）
（3）深入探究
“慎密”小组在“创新”小组的基础上提出：如图3，若
，在角的外部作射线，再分别作和的角平分线，，若，则__________
．（直接写出结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在综合与实践课上，老师请同学们以“两条平行线
，
和一块含
角的直角三角尺
（
，
）”为主题开展数学活动．
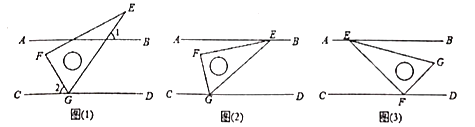
（1）如图（1），把三角尺的角的顶点
放在上，若
，求
的度数；
（2）如图（2），小颖把三角尺的两个锐角的顶点
、分别放在和上，请你探索并说明
与
之间的数量关系；
（3）如图（3），小亮把三角尺的直角顶点
放在上，
角的顶点落在上．若
，
，请用含
，
的式子直接表示
与
的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两城相距800千米，一辆客车从甲城开往乙城，车速为
千米
小时，同时一辆出租车从乙城开往甲城，车速为90千米小时，设客车行驶时间为
小时
当
时，客车与乙城的距离为多少千米
用含a的代数式表示
已知
，丙城在甲、乙两城之间，且与甲城相距260千米
求客车与出租车相距100千米时客车的行驶时间；列方程解答
已知客车和出租车在甲、乙之间的服务站M处相遇时，出租车乘客小王突然接到开会通知，需要立即返回，此时小王有两种返回乙城的方案：
方案一：继续乘坐出租车到丙城，加油后立刻返回乙城，出租车加油时间忽略不计；
方案二：在M处换乘客车返回乙城．
试通过计算，分析小王选择哪种方案能更快到达乙城？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图已知∠1与线段a，用直尺和圆规按下列步骤作图（保留作图痕迹，不写做法。）
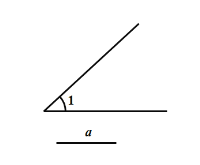
(1)作等∠A于∠1
(2)在∠A的两边分别作AM=AN=a
(3)连接MN
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为保持水土，美化环境，W中学准备在从校门口到柏油公路的这一段土路的两侧栽一些树，并要求土路两侧树的棵数相等间距也相等，且首、尾两端均栽上树，现在学校已备好一批树苗，若间隔30米栽一棵，则缺少22棵；若间隔35米栽一棵，则缺少14棵
（1）求学校备好的树苗棵数．
（2）某苗圃负责人听说W中学想在校外土路两旁栽树的上述情况后，觉得两树间距太大，既不美观，又影响防风固沙的效果，决定无偿支援W中学300棵树苗．请问，这些树苗加上学校自己备好的树苗，间隔5米栽一棵，是否够用？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
，
，点D在边BC上
与B，C不重合
，四边形ADEF为正方形，过点F作
，交CA的延长线于点G，连接FB，交DE于点Q，得出以下结论：
；
：2；
；
其中正确结论的个数是
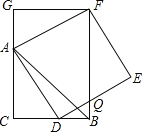
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某机动车出发前油箱内有油42L，行驶若干小时后，在途中加油站加油若干升．油箱中余油量Q（L）与行驶时间t（h）之间的函数关系如图所示，根据如图回答问题：
（1）机动车行驶几小时后加油？加了多少油？
（2）请求出加油前油箱余油量Q与行驶时间t之间的关系式；
（3）如果加油站离目的地还有230km，车速为40km/h，要到达目的地，油箱中的油是否够用？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A（－2，2），B（8，12）在抛物线y=ax2+bx上.
（1）求抛物线的解析式；
（2）如图1，点F的坐标为（0，m）（m>4），直线AF交抛物线于另一点G，过点G作x轴的垂线，垂足为H，设抛物线与x轴的正半轴交于点E，连接FH、AE，求
之值（用含m的代数式表示）；
（3）如图2，直线AB分别交x轴、y轴于C、D两点，点P从点C出发，沿射线CD方向匀速运动，速度为每秒
个单位长度，同时点Q从原点O出发，沿x轴正方向匀速运动，速度为每秒1个单位长度，点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM＝3PM，求t的值.
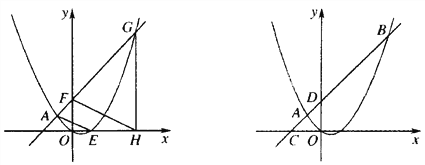
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
