
����Ŀ���ۺ���ʵ��
�����龳
����ѧ����ϣ���ʦ��ͬѧ���ԡ��߶���ǵĹ��ԡ�Ϊ���չ��ѧ��������߶ε��е�ĸ�����ǵ�ƽ���ߵĸ������ƣ����������ڼ���ķ�����Ҳ������֮��������֮�����Ŀ����ת�����ⷨ���Ի���������ͼ1����![]() ���߶�
���߶�![]() �ϵ�һ�㣬
�ϵ�һ�㣬![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ���е㣮
���е㣮
![]()
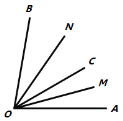
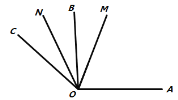
ͼ1 ͼ2 ͼ3
��1������̽��
����![]() ��
��![]() ����
����![]() �ij��ȣ���д��������̣�
�ij��ȣ���д��������̣�
����![]() ��
��![]() ����
����![]() ___________����ֱ��д�������
___________����ֱ��д�������
��2������̽��
�����¡�С���ͬѧ����뵽����ͼ2����֪![]() ���ڽǵ��ڲ�������
���ڽǵ��ڲ�������![]() ���ٷֱ���
���ٷֱ���![]() ��
��![]() �Ľ�ƽ����
�Ľ�ƽ����![]() ��
��![]() ��
��
����![]() ����
����![]() �Ķ�������д��������̣�
�Ķ�������д��������̣�
����![]() ����
����![]() _____________
_____________![]() ����ֱ��д�������
����ֱ��д�������
��3������̽��
�����ܡ�С���ڡ����¡�С��Ļ������������ͼ3����![]() ���ڽǵ��ⲿ������
���ڽǵ��ⲿ������![]() ���ٷֱ���
���ٷֱ���![]() ��
��![]() �Ľ�ƽ����
�Ľ�ƽ����![]() ��
��![]() ����
����![]() ����
����![]() __________
__________![]() ����ֱ��д�������
����ֱ��д�������
���𰸡���1����3����![]() ����2����40
����2����40![]() ����40����3��
����40����3��![]()
��������
��1���������BC���ٸ����е����AM��BN���������MN�ij���
�����âٵķ�����MN���ɣ�
��2�����������BOC�������ý�ƽ���ߵ����������AOM����BON�����������MON��
�����â۵ķ��������MON�Ķ�����
��3���������BOC�����ý�ƽ���ߵ����ʷֱ������AOM����BON���ٸ��ݽǶȵĹ�ϵ����𰸼���.
��1���١�![]() ��
��![]() ��
��
��BC=AB-AC=4��
��![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ���е㣮
���е㣮
��![]() ��
�� ![]() ��
��
��MN=AB-AM-BN=6-1-2=3��
�ڡ�![]() ��
��![]() ��
��
��BC=AB-AC=a-b��
��![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ���е㣮
���е㣮
��![]() ��
��![]() ��
��
��MN=AB-AM-BN=![]() =
=![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2���ۡ�![]() ��
��![]() ��
��
���BOC=��AOB-��AOC=50![]() ��
��
��![]() ��
��![]() �ֱ�ƽ��
�ֱ�ƽ��![]() ��
��![]() ��
��
���AOM=15![]() ����BON=25
����BON=25![]() ��
��
���MON=��AOB-��AOM-��BON=40![]() ��
��
�ܡ�![]() ��
��![]() ��
��
���BOC=(80-m)![]() ��
��
��![]() ��
��![]() �ֱ�ƽ��
�ֱ�ƽ��![]() ��
��![]() ��
��
���AOM=![]() ����BON=��40-
����BON=��40-![]() m��
m��![]() ��
��
���MON=��AOB-��AOM-��BON=40![]() ,
,
�ʴ�Ϊ��40��
��3����![]() ��
��![]() ��
��
���BOC=��AOC-��AOB=(m-n)![]() ��
��
��![]() ��
��![]() �Ľ�ƽ���߷ֱ���
�Ľ�ƽ���߷ֱ���![]() ��
��![]() ��
��
���AOM=![]() ,��CON=
,��CON=![]() ��
��
���MON=��AOC-��AOM-��CON=![]() ��
��
�ʴ�Ϊ��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
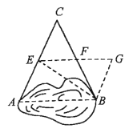
����Ŀ����ͼ��ʾ��Ҫ����һ������ˮ̶�Ŀ��ȣ������ڲ���ֱ�Ӳ�����С�������������ģ�����ƽ����ѡȡһ��C���õ����ֱ�ӵ���A��B�㣬����������AC��BC�ľ��룬���ҳ�AC��BC���е�E��F������EF������EF�ij�����������֪����ˮ̶AB�ij�����2EF��С���������е�����˵�����ɣ��㻹�б�С�����ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
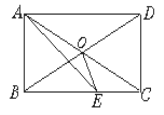
����Ŀ����ͼ���ھ���ABCD�У�AC��BD�ཻ��O��AEƽ�֡�BAD����BC��E������CAE=15�������BOE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С��ͬѧ�ⷽ�̵Ĺ��̣�����ϸ�Ķ������������������⣮
![]()
�⣺ȥ��ĸ����![]() ����
����
ȥ���ţ���![]() ����
����
�����![]() ����
����
�ϲ�ͬ�����![]() ����
����
ϵ����Ϊ![]() ����
����![]() ����
����
��1����������֪��С���Ľ�������________������ţ��������˴����ִ����ԭ����Υ����__________��
A����ʽ�Ļ�������![]() ��B����ʽ�Ļ�������
��B����ʽ�Ļ�������![]() ��C��ȥ���ŷ���D�ӷ������ɣ�
��C��ȥ���ŷ���D�ӷ������ɣ�
��2������д����ȷ�Ľ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=4��BC=6����B=60�㣬����ABC������BC�ķ���ƽ�ƣ��õ���A��B��C�䣬�ٽ���A��B��C���Ƶ�A����ʱ����תһ���ǶȺ�B��ǡ�����C�غϣ���ƽ�Ƶľ������ת�ǵĶ����ֱ�Ϊ��������

A��4��30�� B��2��60�� C��1��30�� D��3��60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ���ϵ��е㣬��
���ϵ��е㣬��![]() ��
��![]() �ϵ�һ���㣨�����
�ϵ�һ���㣨�����![]() �غϣ����ӳ�
�غϣ����ӳ�![]() ������
������![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��
��

![]() ��֤���ı���
��֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
![]() ��գ�����
��գ�����![]() ________ʱ���ı���
________ʱ���ı���![]() �Ǿ��Σ�����
�Ǿ��Σ�����![]() ________ʱ���ı���
________ʱ���ı���![]() �����Σ�
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ����ѧѧ����ѧϰ�������������ʡ����ߺ�һ��ʱ
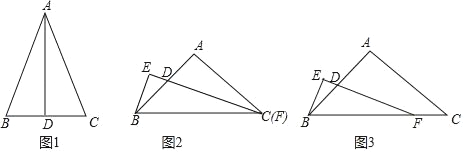
��1����̽�����֣���ͼ1���ڡ�ABC�У���ADƽ�֡�BAC��AD��BCʱ�����Եó�AB��AC��DΪBC�е㣬������ѧ֪ʶ֤���˽��ۣ�
��2����ѧ�����ã����Rt��BEF�͵���Rt��ABC��һ�������Ķ���B����ͼ2��������C�붥��FҲ�غϣ��ҡ�BFE��![]() ��ACB����̽���߶�BE��FD��������ϵ����֤����
��ACB����̽���߶�BE��FD��������ϵ����֤����
��3������չӦ�ã���ͼ3��������C�붥��F���غϣ����ǡ�BFE��![]() ��ACB��Ȼ��������ѧ�����ã��еĽ��ۻ�������֤����Ľ��ۣ�
��ACB��Ȼ��������ѧ�����ã��еĽ��ۻ�������֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1��������ֵ: 2(x2y��xy)��3(x2y��xy)��4x2y������x��-1��y��![]() .
.
��2�����:��ʦ�ںڰ�����д��һ����ȷ��������̣������������ס��һ������ʽ����ʽ���£�![]() ��(��3x2��5x��7)����2x2��3x��6.������Ķ���ʽ.
��(��3x2��5x��7)����2x2��3x��6.������Ķ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �������������ϣ�
�������������ϣ�![]() ���������������غϣ���������
���������������غϣ���������![]() ��
��![]() �ֱ��̶�
�ֱ��̶�![]() ��
��![]() ����
����![]() �Ƶ�
�Ƶ�![]() ��ʱ�뷽����ת��
��ʱ�뷽����ת��![]() �����н��ۣ�
�����н��ۣ�
��![]() ��
��
��������![]() �����̶�
�����̶�![]() ����
����![]() ��
��![]() ������
������
����![]() ��������
��������![]() �����̶�45��
�����̶�45��
������ȷ���ǣ� ��
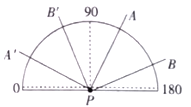
A.�٢�B.�٢�C.�ڢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com