
【题目】如图,△ABC中,∠BAC=120°,AB=AC=6.P是底边BC上的一个动点(P与B、C不重合),以P为圆心,PB为半径的⊙P与射线BA交于点D,射线PD交射线CA于点E.
(1)若点E在线段CA的延长线上,设BP=x,AE=y,求y关于x的函数关系式,并写出x的取值范围.
(2)当BP=![]() 时,试说明射线CA与⊙P是否相切.
时,试说明射线CA与⊙P是否相切.
(3)连接PA,若S△APE=![]() S△ABC,求BP的长.
S△ABC,求BP的长.

【答案】(1)![]() (0<x<
(0<x<![]() );(2)相切;(3)
);(2)相切;(3)![]() 或
或![]() 或
或![]() .
.
【解析】(1)过A作AF⊥BC于F,过P作PH⊥AB于H,∵∠BAC=120°,AB=AC=6,∴∠B=∠C=30°,∵PB=PD,∴∠PDB=∠B=30°,CF=ACcos30°=6×![]() =
=![]() ,∴∠ADE=30°,∴∠DAE=∠CPE=60°,∴∠CEP=90°,∴CE=AC+AE=6+y,∴PC=
,∴∠ADE=30°,∴∠DAE=∠CPE=60°,∴∠CEP=90°,∴CE=AC+AE=6+y,∴PC=![]() =
=![]() ,∵BC=
,∵BC=![]() ,∴PB+CP=
,∴PB+CP= ![]() =
=![]() ,∴
,∴![]() ,∵BD=2BH=
,∵BD=2BH=![]() x<6,∴x<
x<6,∴x<![]() ,∴x的取值范围是0<x<
,∴x的取值范围是0<x<![]() ;
;
(2)相切.理由如下:
∵BP=![]() ,∴CP=
,∴CP=![]() ,∴PE=
,∴PE=![]() PC=
PC=![]() =PB,∴射线CA与⊙P相切;
=PB,∴射线CA与⊙P相切;
(3)当D点在线段BA上时,连接AP,∵S△ABC=![]() BCAF=
BCAF=![]() =
=![]() ,∵S△APE=
,∵S△APE=![]() AEPE=
AEPE=![]() y
y![]() ×(6+y)=
×(6+y)=![]() S△ABC=
S△ABC=![]() ,解得:y=
,解得:y=![]() ,代入
,代入![]() 得x=
得x=![]() .
.
当D点BA延长线上时,PC=![]() EC=
EC=![]() (6﹣y),∴PB+CP=x+
(6﹣y),∴PB+CP=x+![]() (6﹣y)=
(6﹣y)=![]() ,∴
,∴![]() ,∵∠PEC=90°,∴PE=
,∵∠PEC=90°,∴PE=![]() =
=![]() =
=![]() (6﹣y),∴S△APE=
(6﹣y),∴S△APE=![]() AEPE=
AEPE=![]() x=
x=![]() y
y![]() (6﹣y)=
(6﹣y)=![]() S△ABC=
S△ABC=![]() ,解得y=
,解得y=![]() 或
或![]() ,代入
,代入![]() 得x=
得x=![]() 或
或![]() .
.
综上可得,BP的长为![]() 或
或![]() 或
或![]() .
.



科目:初中数学 来源: 题型:
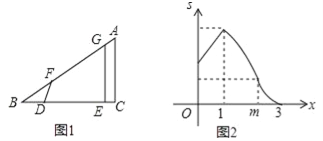
【题目】如图1,△ABC中,∠C=90°,线段DE在射线BC上,且DE=AC,线段DE沿射线BC运动,开始时,点D与点B重合,点D到达点C时运动停止,过点D作DF=DB,与射线BA相交于点F,过点E作BC的垂线,与射线BA相交于点G.设BD=x,四边形DEGF与△ABC重叠部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤m,1<x≤m,m<x≤3时,函数的解析式不同).
(1)填空:BC的长是 ;
(2)求S关于x的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区便民超市为了了解顾客的消费情况,在该小区居民中进行调查,询问每户人家每周到超市的次数,下图是根据调查结果绘制的,请问:
(1)这种统计图通常被称为什么统计图?
(2)此次调查共询问了多少户人家?
(3)超过半数的居民每周去多少次超市?
(4)请将这幅图改为扇形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上,OC=8,OE=17,抛物线![]() 与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
与y轴相交于点A,抛物线的对称轴与x轴相交于点B,与CD交于点K.
(1)将矩形OCDE沿AB折叠,点O恰好落在边CD上的点F处.
①点B的坐标为( 、 ),BK的长是 ,CK的长是 ;
②求点F的坐标;
③请直接写出抛物线的函数表达式;
(2)将矩形OCDE沿着经过点E的直线折叠,点O恰好落在边CD上的点G处,连接OG,折痕与OG相交于点H,点M是线段EH上的一个动点(不与点H重合),连接MG,MO,过点G作GP⊥OM于点P,交EH于点N,连接ON,点M从点E开始沿线段EH向点H运动,至与点N重合时停止,△MOG和△NOG的面积分别表示为S1和S2,在点M的运动过程中,S1S2(即S1与S2的积)的值是否发生变化?若变化,请直接写出变化范围;若不变,请直接写出这个值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
甲、乙两人同时从相距25千米的A地去B地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( ) 
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是(填写序号). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com