
【题目】列方程解应用题
甲、乙两人同时从相距25千米的A地去B地,甲骑车乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40分钟,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好3小时,求两人的速度各是多少?
科目:初中数学 来源: 题型:
【题目】某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106](即96≤净重≤106),样本数据分组为[96,98)(即96≤净重<98)以下类似,[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是 ( ).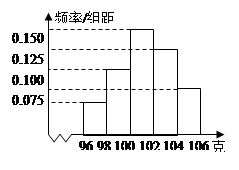
A.90
B.75
C. 60
D.45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是( ) 
A.(0,0)
B.(0,1)
C.(0,2)
D.(0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④DA平分∠CDE;⑤S△ABD:S△ACD=AB:AC.其中,正确的有个. 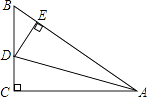
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市教育局倡导的“阳光体育运动”的号召,全校学生积极参与体育运动.为了进一步了解学校九年级学生的身体素质情况,体育老师在九年级800名学生中随机抽取50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,如下所示:
组别 | 次数x | 频数(人数) |
第1组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
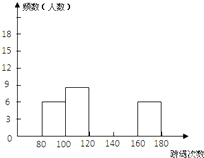
请结合图表完成下列问题:
(1)表中的a=;
(2)请把频数分布直方图补充完整;
(3)这个样本数据的中位数落在第组;
(4)若九年级学生一分钟跳绳次数(x)达标要求是:x<120为不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.根据以上信息,请你估算学校九年级同学一分钟跳绳次数为优的人数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=120°,AB=AC=6.P是底边BC上的一个动点(P与B、C不重合),以P为圆心,PB为半径的⊙P与射线BA交于点D,射线PD交射线CA于点E.
(1)若点E在线段CA的延长线上,设BP=x,AE=y,求y关于x的函数关系式,并写出x的取值范围.
(2)当BP=![]() 时,试说明射线CA与⊙P是否相切.
时,试说明射线CA与⊙P是否相切.
(3)连接PA,若S△APE=![]() S△ABC,求BP的长.
S△ABC,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( ) 
A.35°
B.45°
C.55°
D.65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD. 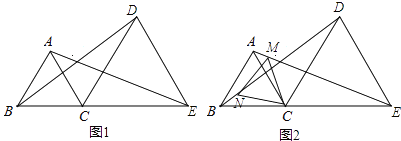
(1)求证:BD=AE;
(2)如图2,若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com