
ЎҫМвДҝЎҝОӘПмУҰКРҪМУэҫЦі«өјөДЎ°Сф№вМеУэФЛ¶ҜЎұөДәЕХЩЈ¬И«РЈС§Йъ»эј«ІОУлМеУэФЛ¶ҜЈ®ОӘБЛҪшТ»ІҪБЛҪвѧУҫЕДкј¶С§ЙъөДЙнМеЛШЦКЗйҝцЈ¬МеУэАПКҰФЪҫЕДкј¶800ГыС§ЙъЦРЛж»ъійИЎ50О»С§ЙъҪшРРТ»·ЦЦУМшЙюҙОКэІвКФЈ¬ТФІвКФКэҫЭОӘСщұҫЈ¬»жЦЖіцІҝ·ЦЖөКэ·ЦІјұнәНІҝ·ЦЖөКэ·ЦІјЦұ·ҪНјЈ¬ИзПВЛщКҫЈә
Чйұр | ҙОКэx | ЖөКэЈЁИЛКэЈ© |
өЪ1Чй | 80ЎЬxЈј100 | 6 |
өЪ2Чй | 100ЎЬxЈј120 | 8 |
өЪ3Чй | 120ЎЬxЈј140 | a |
өЪ4Чй | 140ЎЬxЈј160 | 18 |
өЪ5Чй | 160ЎЬxЈј180 | 6 |
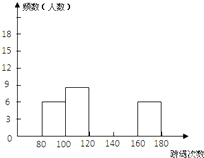
ЗлҪбәПНјұнНкіЙПВБРОКМвЈә
ЈЁ1Ј©ұнЦРөДa=Ј»
ЈЁ2Ј©Зл°СЖөКэ·ЦІјЦұ·ҪНјІ№ідНкХыЈ»
ЈЁ3Ј©ХвёцСщұҫКэҫЭөДЦРО»КэВдФЪөЪЧйЈ»
ЈЁ4Ј©ИфҫЕДкј¶С§ЙъТ»·ЦЦУМшЙюҙОКэЈЁxЈ©ҙпұкТӘЗуКЗЈәxЈј120ОӘІ»әПёсЈ»120ЎЬxЈј140ОӘәПёсЈ»140ЎЬxЈј160ОӘБјЈ»xЎЭ160ОӘУЕЈ®ёщҫЭТФЙПРЕПўЈ¬ЗлДг№АЛгѧУҫЕДкј¶Н¬С§Т»·ЦЦУМшЙюҙОКэОӘУЕөДИЛКэОӘ Ј®
Ўҫҙр°ёЎҝ
ЈЁ1Ј©12
ЈЁ2Ј©ҪвЈәУЙЈЁ1Ј©өГТ»·ЦЦУМшЙюҙОКэФЪ120ЎЬxЈј140·¶О§ЦРөДИЛКэОӘ12Ј¬¶шТ»·ЦЦУМшЙюҙОКэФЪ140ЎЬxЈј160·¶О§ЦРөДИЛКэОӘ18ИЛЈ¬І№И«ЖөВКЦұ·ҪНіјЖНјјҙҝЙ
ЈЁ3Ј©3
ЈЁ4Ј©96
ЎҫҪвОцЎҝҪвЈәЈЁ1Ј©УЙМвТвөГЈәa=50-ЈЁ6+8+18+6Ј©=12Ј»ЈЁ3Ј©ЎЯa=12Ј¬
Ўа6+8+12=26Ј¬ФтХвёцСщұҫКэҫЭөДЦРО»КэВдФЪөЪ3РЎЧйЦРЈ»ЈЁ4Ј©УЙұнёсөГЈә50ИЛЦРТ»·ЦЦУМшЙюҙОКэФЪ160ЎЬxЈј180·¶О§ЦРөДИЛКэОӘ6ИЛЈ¬јҙУЕРгөДИЛКэОӘ6ИЛЈ¬
ФтСщұҫЦРУЕРгИЛКэЛщХјөД°Щ·ЦұИОӘ ![]() =12%Ј¬
=12%Ј¬
Фт800ГыС§ЙъЦРУЕРгөДИЛКэОӘ800ЎБ12%=96ИЛЈ®
ЈЁ1Ј©ёщҫЭЧЬКэ=ёчЖөКэЦ®әНҝЙЗуҪвЈ»ЈЁ2Ј©ёщҫЭЖөКэ·ЦІјұнЦРөДРЕПўҝЙІ№ідНкХыЖөКэ·ЦІјЦұ·ҪНјЈ»ЈЁ3Ј©ёщҫЭЦРО»КэөД¶ЁТеҝЙЗуЈ»ЈЁ4Ј©800ГыС§ЙъЦРУЕРгөДИЛКэ=800![]() °Щ·ЦКэЎЈ
°Щ·ЦКэЎЈ



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
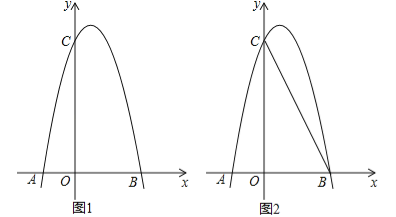
ЎҫМвДҝЎҝИзНј1Ј¬¶ФіЖЦбОӘЦұПЯx=![]() өДЕЧОпПЯҫӯ№эBЈЁ2Ј¬0Ј©ЎўCЈЁ0Ј¬4Ј©БҪөгЈ¬ЕЧОпПЯУлxЦбөДБнТ»Ҫ»өгОӘAЈ®
өДЕЧОпПЯҫӯ№эBЈЁ2Ј¬0Ј©ЎўCЈЁ0Ј¬4Ј©БҪөгЈ¬ЕЧОпПЯУлxЦбөДБнТ»Ҫ»өгОӘAЈ®
ЈЁ1Ј©ЗуЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©ИфөгPОӘөЪТ»ПуПЮДЪЕЧОпПЯЙПөДТ»өгЈ¬ЙиЛДұЯРОCOBPөДГж»эОӘSЈ¬ЗуSөДЧоҙуЦөЈ»
ЈЁ3Ј©ИзНј2Ј¬ИфMКЗПЯ¶ОBCЙПТ»¶ҜөгЈ¬ФЪxЦбКЗ·сҙжФЪХвСщөДөгQЈ¬К№ЎчMQCОӘөИСьИэҪЗРОЗТЎчMQBОӘЦұҪЗИэҪЗРОЈҝИфҙжФЪЈ¬ЗуіцөгQөДЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЎчABCЦРЈ¬ЎПABCУлЎПACBөДЖҪ·ЦПЯҪ»УЪөгFЈ¬№эөгFЧчDEЎОBCҪ»ABУЪөгDЈ¬Ҫ»ACУЪөгEЈ¬ДЗГҙПВБРҪбВЫЈә ўЩЎчBDFәНЎчCEF¶јКЗөИСьИэҪЗРОЈ»ўЪDE=BD+CEЈ»ўЫЎчADEөДЦЬіӨөИУЪABУлACөДәНЈ»ўЬBF=CFЈ®ЖдЦРХэИ·өДУР Ј® ЈЁМоХэИ·өДРтәЕЈ©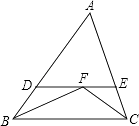
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘТ»ёцТ»ФӘ¶юҙО·ҪіМөДТ»ёцёщОӘ3Ј¬¶юҙОПоПөКэКЗ1Ј¬ФтХвёцТ»ФӘ¶юҙО·ҪіМҝЙТФКЗ_____ЈЁЦ»РиРҙіцТ»ёц·ҪіМјҙҝЙЈ©
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝБР·ҪіМҪвУҰУГМв
јЧЎўТТБҪИЛН¬КұҙУПаҫа25З§ГЧөДAөШИҘBөШЈ¬јЧЖпіөТТІҪРРЈ¬јЧөДЛЩ¶ИКЗТТөДЛЩ¶ИөД3ұ¶Ј¬јЧөҪҙпBөШНЈБф40·ЦЦУЈ¬И»әуҙУBөШ·ө»ШAөШЈ¬ФЪНҫЦРУцјыТТЈ¬ХвКұҫаЛыГЗіц·ўөДКұјдЗЎәГ3РЎКұЈ¬ЗуБҪИЛөДЛЩ¶ИёчКЗ¶аЙЩЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
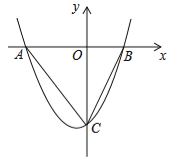
ЎҫМвДҝЎҝИзНјЈ¬ЕЧОпПЯ![]() ЈЁaЎЩ0Ј©УлxЦбҪ»УЪөгAЈЁ©Ғ5Ј¬0Ј©әНөгBЈЁ3Ј¬0Ј©Ј¬УлyЦбҪ»УЪөгCЈ®
ЈЁaЎЩ0Ј©УлxЦбҪ»УЪөгAЈЁ©Ғ5Ј¬0Ј©әНөгBЈЁ3Ј¬0Ј©Ј¬УлyЦбҪ»УЪөгCЈ®
ЈЁ1Ј©ЗуёГЕЧОпПЯөДҪвОцКҪЈ»
ЈЁ2Ј©ИфөгEОӘxЦбПВ·ҪЕЧОпПЯЙПөДТ»¶ҜөгЈ¬өұSЎчABE=SЎчABCКұЈ¬ЗуөгEөДЧшұкЈ»
ЈЁ3Ј©ФЪЈЁ2Ј©өДМхјюПВЈ¬ЕЧОпПЯЙПКЗ·сҙжФЪөгPЈ¬К№ЎПBAP=ЎПCAEЈҝИфҙжФЪЈ¬ЗуіцөгPөДәбЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ФЪRtЎчABCЦРЈ¬DЈ¬EОӘРұұЯABЙПөДБҪёцөгЈ¬ЗТBD=BCЈ¬AE=ACЈ¬ФтЎПDCEөДҙуРЎОӘЈЁ¶ИЈ©Ј® 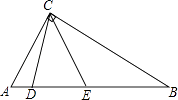
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЦұПЯABЎўCDПаҪ»УЪөгO.
ЈЁ1Ј©OEЎўOF·ЦұрКЗЎПAOCЎўЎПBODөДЖҪ·ЦПЯ.»ӯіцХвёцНјРО.
ЈЁ2Ј©ЙдПЯOEЎўOFФЪН¬Т»МхЦұПЯЙПВр?(ЦұҪУРҙіцҪбВЫ)
ЈЁ3Ј©»ӯЎПAODөДЖҪ·ЦПЯOG.OEУлOGУРКІГҙО»ЦГ№ШПө?ІўЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com