
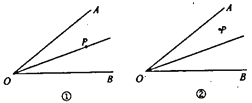
【题目】如图①,OP是∠AOB的平分线。请过点P画一条直线,在∠AOB上截得一个等腰三角形,又如图②,如果点P是任命的一点,那么能否过这一点画一条直线,也在∠AOB上截得一个等腰三角形呢?请你画一画。
【答案】图略,能,图略
【解析】试题分析:(1)如图,直线CD为过点P的一条垂线且垂足为P,则△OCD是等腰三角形;(3)如图,过点O作∠AOB的角平分线OD,过点P作PD⊥OD于点D,延长交OA,OB于点M,N,则△OMN为等腰三角形.
试题解析:
(1)如图,直线CD为过点P的一条垂线且垂足为P,则△OCD是等腰三角形.

∵OP为∠AOB的角平分线
∴∠AOP=∠BOP
∵∠CPO=∠DPO=90°,OP=OP
∴△COP≌△DOP(ASA)
∴OC=OD
∴△OCD是等腰三角形.
(2)如图,过点O作∠AOB的角平分线OD,过点P作PD⊥OD于点D,延长交OA,OB于点M,N,则△OMN为等腰三角形.
∵OD为∠AOB的角平分线

∴∠AOD=∠BOD
∵∠MPO=∠NPO=90°,OD=OD
∴△MOD≌△NOD(ASA)
∴OM=ON
∴△OMN是等腰三角形.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点B位于y轴的左侧,到x轴的距离是4个单位长度,到y轴的距离是5个单位长度,则点B的坐标是( )
A.(﹣5,4)B.(﹣4,5)
C.(﹣5,4)或(﹣5,﹣4)D.(﹣4,5)或(﹣4,﹣5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市“艺术节”期间,小明、小亮都想去观看茶艺表演,但是只有一张茶艺表演门票,他们决定采用抽卡片的办法确定谁去.规则如下:将正面分别标有数字1、2、3、4的四张卡片(除数字外其余都相同)洗匀后,背面朝上放置在桌面上,随机抽出一张记下数字后放回;重新洗匀后背面朝上放置在桌面上,再随机抽出一张记下数字.如果两个数字之和为奇数,则小明去;如果两个数字之和为偶数,则小亮去.你认为这个规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠B=30°,CD为AB边上的高,E是AB上一点,且CE=BE.
(1)写出图中所有的等腰三角形:______________________________
(2)写出图中所有的等边三角形:______________________________
(3)若DE=2cm,则AB=______cm,AC=______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年5月25日,中国国际大数据产业博览会在贵阳会展中心开幕,博览会设了编号为1~6号展厅共6个,小雨一家计划利用两天时间参观其中两个展厅:第一天从6个展厅中随机选择一个,第二天从余下的5个展厅中再随机选择一个,且每个展厅被选中的机会均等.
(1)第一天,1号展厅没有被选中的概率是 ;
(2)利用列表或画树状图的方法求两天中4号展厅被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个两位数,把它的个位数字与十位数字交换位置得到新两位数,原两位数的个位数字比原两位数的十位数字大2,且新两位数与原两位数的和为154,求原两位数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+6与反比例函数y=![]() (k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(k>0)的图象交于点A(1,m),与x轴交于点B,平行于x轴的直线y=n(0<n<6)交反比例函数的图象于点M,交AB于点N,连接BM.
(1)求m的值和反比例函数的表达式;
(2)直线y=n沿y轴方向平移,当n为何值时,△BMN的面积最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() (k≠0)的图象是__________,当k>0时,图象的两个分支分别在第__________、__________象限内,在每个象限内,y随x的增大而__________;当k<0时,图象的两个分支分别在第__________、__________象限内,在每个象限内,y随x的增大而__________;
(k≠0)的图象是__________,当k>0时,图象的两个分支分别在第__________、__________象限内,在每个象限内,y随x的增大而__________;当k<0时,图象的两个分支分别在第__________、__________象限内,在每个象限内,y随x的增大而__________;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com