
【题目】如图,△ABC为等边三角形,∠BAD=∠ACF=∠CBE,求∠DEC的度数。

【答案】120°
【解析】试题分析:根据等边三角形的性质和已知条件易证△ACF≌△CBE≌△BAD,再由等边三角形的性质和等边三角形的判定方法易证△DEF为等边三角形,可得∠DEF =60°,根据平角的定义即可求得∠DEC的度数.
试题解析:
∵△ABC为等边三角形,
∴AB=AC=BC,∠BAC=∠ABC=∠ACB;
又∵∠BAD=∠CBE=∠ACF,
∴∠BAC-∠BAD=∠ABC-∠CBE=∠ACB-∠ACF,
∴∠CAF=∠ABE=∠BCE,
∴△ACF≌△CBE≌△BAD(ASA).
∴AF=BD=CE,AD=BE=CF,
∴AD-AF=BE-BD=CF-CE,
∴DF=DE=EF,
∴△DEF为等边三角形,
∴∠DEF=∠DFE=∠EDF=60°,
又 点C点F点E三点共线,
∴∠DEC=120°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=AC,∠BCA=90°,P为直线AC上一点,过点A作AD⊥BP于点D,交直线BC于点Q.
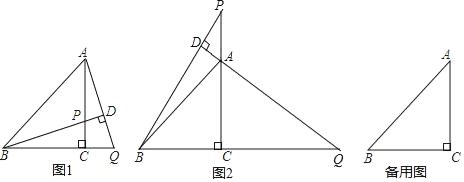
(1)如图1,当P在线段AC上时,求证:BP=AQ;
(2)如图2,当P在线段CA的延长线上时,(1)中的结论是否成立? (填“成立”或“不成立”)
(3)在(2)的条件下,当∠DBA= 度时,存在AQ=2BD,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.

(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,OP是∠AOB的平分线。请过点P画一条直线,在∠AOB上截得一个等腰三角形,又如图②,如果点P是任命的一点,那么能否过这一点画一条直线,也在∠AOB上截得一个等腰三角形呢?请你画一画。
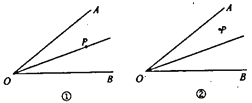
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家购进A、B两种商品,A种商品用了480元,B种商品用了1260元,A、B两种商品的数量比为1﹕3,A种商品每千克的进价比B种商品每千克的进价多2元.A、B两种商品各购进多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国制造”是世界上认知度最高的标签之一,因此,我县越来越多的群众选择购买国产空调,已知购买1台A型号的空调比1台B型号的空调少200元,购买2台A型号的空调与3台B型号的空调共需11200元,求A、B两种型号的空调的购买价各是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com