
【题目】荣昌公司要将本公司100吨货物运往某地销售,经与春晨运输公司协商,计划租用甲,乙两种型号的汽车共6辆,用这6辆汽车一次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨.已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元;租用2辆甲型汽车和1辆乙型汽车共需费用2450元,且同一种型号汽车每辆租车费用相同.
(1)求租用一辆甲型汽车,一辆乙型汽车的费用分别是多少元?
(2)若荣昌公司计划此次租车费用不超过5000元.通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用.
(3)该商业公司生产的此时令商品每件成本为15元,经过市场调研发现,这种商品在未来20天内的日销量m(件)与时间t(天)的函数关系:m=﹣2t+100;该商品每天的价格y(元/件)与时间t(天)的函数关系为:y=![]() t+20(1≤t≤20),其中t取整数;在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润时间t(天)的增大而增大(含20天的日销售利润和第19天的日销售利润相等的情况),求a的最小值.
t+20(1≤t≤20),其中t取整数;在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润时间t(天)的增大而增大(含20天的日销售利润和第19天的日销售利润相等的情况),求a的最小值.
【答案】(1)租用一辆甲型汽车的费用是800元,租用一辆乙型汽车的费用是850元;(2)共有三种方案,分别是:方案一:租用甲型汽车2辆,租用乙型汽车4辆;方案二:租用甲汽车3辆,租用乙型汽车3辆;方案三:租用甲型汽车4辆,租用乙型汽车2辆.最低运费是4900元;(3)a的最小值是![]() .
.
【解析】
(1)找出等量关系列出方程组再求解即可.本题的等量关系为“租用1辆甲型汽车和2辆乙型汽车共需费用2500元”和“租用2辆甲型汽车和1辆乙型汽车共需费用2450元”;
(2)设租用甲型汽车z辆,租用乙型汽车(6-z)辆.根据荣昌公司要将本公司100吨货物运往某地销售,以及计划此次租车费用不超过5000元列出不等式组,求解即可;
(3)设日销售利润为w元,根据w=日销量m×(售价一成本-捐赠),利用对称轴解决问题.
(1)设租用一辆甲型汽车的费用是x元,租用一辆乙型汽车的费用是y元.
由题意得,![]() ;
;
解得:![]() ,
,
答:租用一辆甲型汽车的费用是800元,租用一辆乙型汽车的费用是850元.
(2)设租用甲型汽车z辆,租用乙型汽车(6-z)辆.
由题意得![]() ,
,
解得2≤z≤4,
由题意知,z为整数,
∴z=2或z=3或z=4,
∴共有3种方案,分别是:
方案一:租用甲型汽车2辆,租用乙型汽车4辆;
方案二:租用甲型汽车3辆,租用乙型汽车3辆;
方案三:租用甲型汽车4辆,租用乙型汽车2辆.
方案一的费用是800×2+850×4=5000(元);
方案二的费用是800×3+850×3=4950(元);
方案三的费用是800×4+850×2=4900(元);
∵5000>4950>4900;
∴最低运费是方案三的费用:4900元;
答:共有三种方案,分别是:
方案一:租用甲型汽车2辆,租用乙型汽车4辆;
方案二:租用甲汽车3辆,租用乙型汽车3辆;
方案三:租用甲型汽车4辆,租用乙型汽车2辆.最低运费是4900元.
(3)设日销售利润为w元,
则w=(-2t+100)(![]() t+20-15-a)=-
t+20-15-a)=-![]() t2+(2a+15)t+500-100a,
t2+(2a+15)t+500-100a,
对称轴是:t=2a+15,
∵1≤t≤20,且每天扣除捐赠后的日销售利润时间t(天)的增大而增大,
当x=19与x=20是对称点时,t=19.5,
∴2a+15≥19.5,
a≥![]() ,
,
∵a<4,
∴![]() ≤a<4,
≤a<4,
∴a的最小值是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线![]() 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).

(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20 km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1 、y2 (km), y1 、y2 与x的函数关系如图所示.
(1)求y2与x的函数关系式;
(2)若两人在出发时都配备了通话距离为3km的对讲机,求甲、乙两人在骑行过程中可以用对讲机通话的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知等边三角形ABC,点P为AB的中点,点D、E分别为边AC、BC上的点,∠APD+∠BPE=60°.
(1)①若PD⊥AC,PE⊥BC,直接写出PD、PE的数量关系:____;
②如图1,证明:AP=AD+BE
(2)如图2,点F、H分别在线段BC、AC上,连接线段PH、PF,若PD⊥PF且PD=PF,HP⊥EP.求∠FHP的度数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知港口A东偏南10°方向有一处小岛B,一艘货轮从港口A沿南偏东40°航线出发,行驶80海里到达C处,此时观测小岛B在北偏东60°方向.
(1)求此时货轮到小岛B的距离.
(2)在小岛周围36海里范围内是暗礁区,此时轮船向正东方向航行有没有触礁危险?请作出判断并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:
(1)请按照小明的思路完成上述问题:求每个小长方形的面积;
(2)某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是 cm;
(3)小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC.

(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
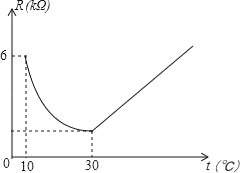
【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加![]() kΩ.
kΩ.
(1)求R和t之间的关系式;
(2)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com