Question

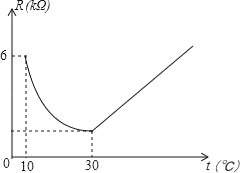
【题目】家用电灭蚊器的发热部分使用了PTC发热材料，它的电阻R（kΩ）随温度t（℃）（在一定范围内）变化的大致图象如图所示．通电后，发热材料的温度在由室温10℃上升到30℃的过程中，电阻与温度成反例关系，且在温度达到30℃时，电阻下降到最小值；随后电阻承温度升高而增加，温度每上升1℃，电阻增加kΩ．

（1）求R和t之间的关系式；

（2）家用电灭蚊器在使用过程中，温度在什么范围内时，发热材料的电阻不超过4kΩ．

Answer 1

【答案】（1）见解析；（2）15℃～37.5℃

【解析】

（1）当10≤t≤30时，是反比例函数，利用待定系数法可求出解析式，然后将t=30℃代入关系式求出此时的R值，然后再根据题意列式即可求出t>30时的函数关系式；

（2）将R=4代入（1）中求得的两个解析式即可求得答案.

（1）∵温度在由室温10℃上升到30℃的过程中，电阻与温度成反比例关系，

∴当10≤t≤30时，设关系为R=，

将（10，6）代入上式中得：6=，解得k=60，

故当10≤t≤30时，R=；

将t=30℃代入上式中得：R==2，

∴温度在30℃时，电阻R=2（kΩ），

∵在温度达到30℃时，电阻下降到最小值，随后电阻随温度升高而增加，温度每上升1℃，电阻增加kΩ，

∴当t≥30时，R=2+（t﹣30）=t﹣6，

故R和t之间的关系式为R= ；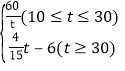

（2）把R=4代入R=t﹣6，得t=37.5，

把R=4代入R=，得t=15，

所以，温度在15℃～37.5℃时，发热材料的电阻不超过4kΩ．