
【题目】如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm,求:
(1)CD的长;
(2)△ABC的角平分线AE交CD于点F,交BC于E点,求证:∠CFE=∠CEF.

科目:初中数学 来源: 题型:
【题目】阅读材料:
小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:
(1)请按照小明的思路完成上述问题:求每个小长方形的面积;
(2)某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是 cm;
(3)小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售,在销售了40千克之后,余下的打七五折全部售完.销售金额y(元)与售出西瓜的千克数x(千克)之间的关系如图所示.下列结论正确的是( )

A.降价后西瓜的单价为2元/千克B.广宇一共进了50千克西瓜
C.售完西瓜后广宇获得的总利润为44元D.降价前的单价比降价后的单价多0.6元
查看答案和解析>>
科目:初中数学 来源: 题型:
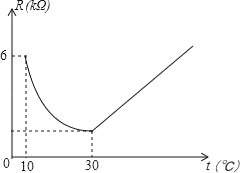
【题目】家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加![]() kΩ.
kΩ.
(1)求R和t之间的关系式;
(2)家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,某商铺经营某种旅游纪念品.该商铺第一次批发购进该纪念品共花费3 000元,很快全部售完.接着,该商铺第二次批发购进该纪念品共花费9000元.已知第二次所购进该纪念品的数量是第一次的2倍还多300个,第二次的进价比第一次的进价提高了20%.
(1)求第一次购进该纪念品的进价是多少元?
(2)若该纪念品的两次售价均为9元/个,两次所购纪念品全部售完后,求该商铺两次共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某木板加工厂将购进的A型、B型两种木板加工成C型,D型两种木板出售,已知一块A型木板的进价比一块B型木板的进价少10元,且购买3块A型木板和2块B型木板共花费120元.
(1)A型木板与B型木板的进价各是多少元?
(2)根据市场需求,该木板加工厂决定用不超过2770元购进A型木板、B型木板共100块,若一块A型木板可制成1块C型木板、2块D型木板;一块B型木板可制成2块C型木板、1块D型木板,且生产出来的C型木板数量不少于D型木板的数量的7/5.
①该木板加工厂有几种进货方案?
②若C型木板每块售价30元,D型木板每块售价25元,且生产出来的C型木板、D型木板全部售出,哪一种方案获得的利润最大,求出最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长方形纸片ABCD沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图1);再沿过点E的直线折叠,使点D落在BE上的点D′处,折痕为EG(如图2);再展平纸片(如图3),则图3中∠α的大小为()
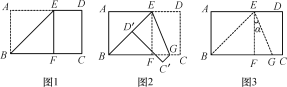
A.30°B.25.5°C.20°D.22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
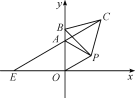
【题目】如图,在平面直角坐标系中,△AOP为等边三角形,A(0,2),点B为y轴上一动点,以BP为边作等边△PBC,延长CA交x轴于点E.
(1)求证:OB=AC;
(2)∠CAP的度数是;
(3)当B点运动时,猜想AE的长度是否发生变化?并说明理由;
(4)在(3)的条件下,在y轴上存在点Q,使得△AEQ为等腰三角形,请写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com