练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．已知关于x的方程$\frac{2m+5}{3}$=$\frac{5x+1}{4}$的解为负数，求m的取值范围．

    分析 解出关于x的方程，根据题意列出关于m的一元一次不等式，解不等式得到答案．

    解答 解：解方程得，x=$\frac{8m+17}{15}$，
    由题意得，$\frac{8m+17}{15}$＜0，
    解得：m＜-$\frac{17}{8}$．

    点评 本题考查的是一元一次方程的解法，正确解出一元一次方程、根据题意得到一元一次不等式并正确解出不等式是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

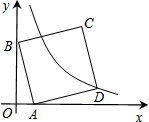    5．如图，在平面直角坐标系中，A（1，0），B（0，3），以AB为边在第一象限作正方形ABCD，点D在双曲线y=$\frac{k}{x}$（k≠0）上，将正方形沿x轴负方向平移m个单位长度后，点C恰好落在双曲线上，则m的值是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

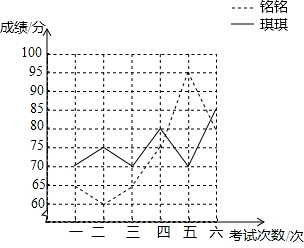    6．铭铭和琪琪的6次生物考试成绩的折线统计图如图所示．
    （1）请根据图示6次生物考试成绩填写下表：
     平均数众数中位数方差
    铭铭757575125
    琪琪757072.533.3
    （2）请你对这两位同学的6次考试成绩进行分析，判断哪位同学的成绩较稳定？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

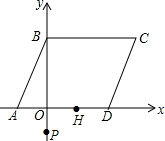    3．如图，?ABCD中，A（-2，0）、B（0，4），AD在x轴上，且OD=2OA．
    （1）求顶点C、D的坐标及CD的长；
    （2）求直线AC的解析式；
    （3）x轴下方的y轴上是否存在点P，使得直线CP把?ABCD的面积分成1：6两部分？若存在，求出P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

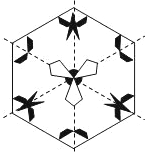    10．学习了旋转对称图形，小明与小东研究如图所示的图案．小明说：“只需要把该图案的$\frac{1}{6}$绕其中心分别旋转60°、120°、180°、240°、300°后，由前后的图形就可以共同组成该图案．”小东说：“错了，应该把该图案的把该图案的$\frac{1}{3}$绕其中心分别旋转120°、240°后，由前后的图形就可以共同组成该图案．”“你说的真对，我是一叶障目，不识泰山啊”．你觉得小东该说什么，请在横线上把小东的补充完整．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．解不等式：3（2-y）＜2（y-2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．某商店一种商品的定价为每件20元，商店为了促销，决定如果购买5件以上，则超过5件的部分打七折．用表达式表示购买这种商品的货款y（元）与购买数量x（件）之间的函数关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．为了探究代数式$\sqrt{{x^2}+4}+\sqrt{{{（{9-x}）}^2}+1}$的最小值，小明巧妙的运用了“数形结合”思想．具体方法是这样的：如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC．已知AB=2，DE=1，BD=9，设BC=x．则$AC=\sqrt{{x^2}+4}$，$CE=\sqrt{{{（{9-x}）}^2}+1}$，则问题即转化成求AC+CE的最小值．
    （1）我们知道当A、C、E在同一直线上时，AC+CE的值最小，于是可求得$\sqrt{{x^2}+4}+\sqrt{{{（{9-x}）}^2}+1}$的最小值等于，3$\sqrt{10}$，此时x=6；
    （2）请你根据上述的方法和结论，试构图求出代数式$\sqrt{{x}^{2}+25}$+$\sqrt{{x}^{2}-24x+153}$的最小值及对应的x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知10m=3，10n=2，求102m+3n的值．

    查看答案和解析>>

    同步练习册答案