
| A. | x2-10x+9=0 | B. | x2+10x+9=0 | C. | x2-10x-9=0 | D. | x2+10x-9=0 |
分析 根据根与系数的关系,甲看错了方程的常数项,得出的两根为8和2,于是一次项系数为-(8+2)=-10,同样,乙看错了一次项的系数,得出两根为-9或-1,于是得到常数项为-9×(-1)=9,然后写出满足条件的方程即可.
解答 解:由于甲看错了方程的常数项,得出的两根为8和2,则一次项系数为-(8+2)=-10,
而乙看错了方程的一次项的系数,得出两根为-9或-1,则常数项为-9×(-1)=9,
所以原一元二次方程为x2-10x+9=0.
故选A.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:选择题
| 尺码/厘米 | 23 | 23.5 | 24 | 24.5 | 25 | 25.5 |
| 销售量/双 | 5 | 10 | 22 | 39 | 56 | 43 |
| A. | 平均数 | B. | 中位数 | C. | 众数 | D. | 加权平均数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
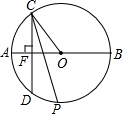 如图,AB为⊙O的直径,从圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,求证:$\widehat{AP}$=$\widehat{BP}$.
如图,AB为⊙O的直径,从圆上一点C作弦CD⊥AB,∠OCD的平分线交⊙O于点P,求证:$\widehat{AP}$=$\widehat{BP}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
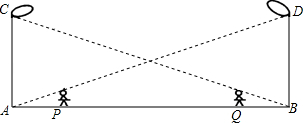 如图所示,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶点刚好接触到路灯AC的底部,当他向前再走行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是多少?
如图所示,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶点刚好接触到路灯AC的底部,当他向前再走行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{24}{x+2}-\frac{20}{x}$=1 | B. | $\frac{20}{x}-\frac{24}{x+2}$=1 | C. | $\frac{24}{x}-\frac{20}{x+2}$=1 | D. | $\frac{20}{x+2}-\frac{24}{x}$=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com