
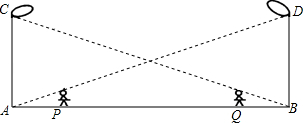
 如图所示,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶点刚好接触到路灯AC的底部,当他向前再走行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是多少?
如图所示,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶点刚好接触到路灯AC的底部,当他向前再走行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是多少? 分析 如图,PM=QN=1.5m,AC=BD=9m,PQ=20m,先证明△APM∽△ABD,利用相似比可得AP=$\frac{1}{6}$AB,同理可得BQ=$\frac{1}{6}$AB,所以$\frac{1}{6}$AB+20+$\frac{1}{6}$AB=AB,然后解关于AB的方程即可.
解答 解:如图,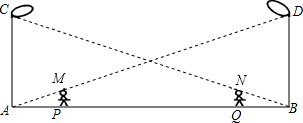 PM=QN=1.5m,AC=BD=9m,PQ=20m,
PM=QN=1.5m,AC=BD=9m,PQ=20m,
∵PM∥BD,
∴△APM∽△ABD,
∴$\frac{PM}{BD}$=$\frac{AP}{AB}$,即$\frac{1.5}{9}$=$\frac{AP}{AB}$,
∴AP=$\frac{1}{6}$AB,
∵QN∥AC,
∴△BQN∽△BAC,
∴$\frac{QN}{AC}$=$\frac{BQ}{BA}$,即$\frac{1.5}{9}$=$\frac{BQ}{BA}$,
∴BQ=$\frac{1}{6}$AB,
而AP+PQ+BQ=AB,
∴$\frac{1}{6}$AB+20+$\frac{1}{6}$AB=AB,
∴AB=30(m).
答:两路灯之间的距离是30m.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-10x+9=0 | B. | x2+10x+9=0 | C. | x2-10x-9=0 | D. | x2+10x-9=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 一辆汽车和一辆摩托车同时分别从A,B两地去同一城市,它们离A地的路程随时间变化的图象如图所示.当汽车到达目的地时,摩托车距目的地20千米.
一辆汽车和一辆摩托车同时分别从A,B两地去同一城市,它们离A地的路程随时间变化的图象如图所示.当汽车到达目的地时,摩托车距目的地20千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 A、B两地相距20千米,甲汽车以80千米/小时的速度从A出发,乙汽车以60千米/小时的速度从B出发,两车同时出发且同向而行,问经过几小时,两车相距40千米?
A、B两地相距20千米,甲汽车以80千米/小时的速度从A出发,乙汽车以60千米/小时的速度从B出发,两车同时出发且同向而行,问经过几小时,两车相距40千米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com