
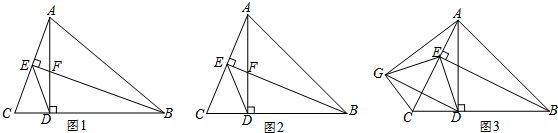
分析 (1)根据勾股定理和直角三角形斜边中线等于斜边的一半即可求解;
(2)过点D作DM⊥ED交BE于点M,先证明△ACD≌△BFD和△AED≌△BMD,进一步通过等量代换和加减即可求解;
(3)过点D作DN⊥ED于点D交BE于点N,先证明△AED≌△BND,再论证四边形DGEN为平行四边形,通过等量代换即可求解.
解答 解:(1)如图1
∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∵AD=3,AB=BC=5,
∴AE=CE,DE=$\frac{1}{2}$AC,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴CD=BC-BD=1,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
∴DE=$\frac{\sqrt{10}}{2}$;
(2)如图2
过点D作DM⊥ED交BE于点M,
∵BE⊥AC于点E,AD⊥BC于点D,
可证:∠CBE=∠CAD,∠EDF=∠BDM,
∵∠ABC=45°,
∴△ADB是等腰直角三角形,
∴AD=BD,
在△ACD和△BFD中,
$\left\{\begin{array}{l}{∠CAD=∠CBE}\\{AD=BD}\\{∠ADC=∠BDF=90°}\end{array}\right.$,
∴△ACD≌△BFD,
∴FD=CD,AC=BF,
在△AED和△BMD中,
$\left\{\begin{array}{l}{∠EAD=DBM}\\{AD=BD}\\{∠EDF=∠BMD}\end{array}\right.$,
∴△AED≌△BMD,
∴DE=DM,AE=BM,
∴FM=CE,
∴EF+EC=EF+FM=EM,
在Rt△DEM中,可求EM=$\sqrt{2}$ED,
∴EF+EC=$\sqrt{2}$ED;
(3)如图3
过点D作DN⊥ED于点D交BE于点N.
与(2)同理易证△AED≌△BND,
∴ED=ND,BN=AE,
∴∠DEB=45°,
∵BE⊥AC,
∴∠CED=∠BED=45°
∴∠CEG=∠CED=45°
∴∠DEG=90°
∴∠DEG=∠EDN=90°
∴EG∥DN,又DG∥BE
∴四边形DGEN为平行四边形
∴DG=EN
∵BE=EN+BN
∴BE=AE+DG.
点评 此题主要考查几何变换的综合问题,会构造三角形全等,会运用勾股定理求线段的长度,会灵活运用等量代换和加减是解题的关键.


科目:初中数学 来源: 题型:解答题
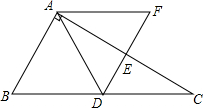 如图,Rt△ABC中,∠BAC=90°,∠C=30°.点D、E分别是边BC、AC的中点,DE的联线与BC的平行线AF交于点F.
如图,Rt△ABC中,∠BAC=90°,∠C=30°.点D、E分别是边BC、AC的中点,DE的联线与BC的平行线AF交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
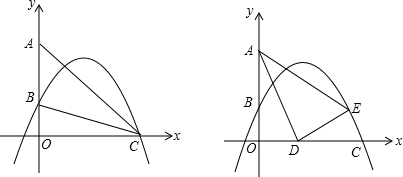
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间 | 负责组别 | 车流总量 | 每分钟车流量 |
| 早晨上学6:30~7:00 | ①② | 2747 | 92 |
| 中午放学11:20~11:50 | ③④ | 1449 | 48 |
| 下午放学5:00~5:30 | ⑤⑥ | 3669 | 122 |
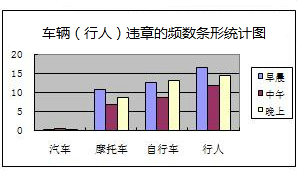 回答下列问题:
回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
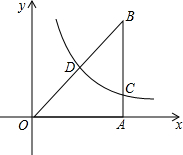 已知,Rt△OAB在直角坐标系内的位置如图所示,BA⊥OA,点B(4,4),反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过线段OB的中点D,且与直线AB交于点C.
已知,Rt△OAB在直角坐标系内的位置如图所示,BA⊥OA,点B(4,4),反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过线段OB的中点D,且与直线AB交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
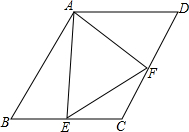 如图,已知菱形ABCD的边长为6cm,∠B=60°,E、F是BC、CD上的两个动点,且∠EAF=60°,试判断四边形AECF的面积是否变化?不变请求值.
如图,已知菱形ABCD的边长为6cm,∠B=60°,E、F是BC、CD上的两个动点,且∠EAF=60°,试判断四边形AECF的面积是否变化?不变请求值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com