
����Ŀ����֪����O�ǵȱߡ�ABC�ڵ���һ�㣬����OA��OB��OC��
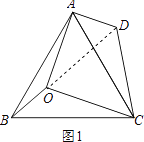
��1����ͼ1����֪��AOB=150�㣬��BOC=120�㣬����BOC�Ƶ�C��˳ʱ�뷽����ת60��á�ADC��
�١�DAO�Ķ����Ƕ��٣�
���õ�ʽ��ʾ�߶�OA��OB��OC֮���������ϵ����֤����
��2�����AOB=������BOC=�£�
�ٵ�����������ʲô��ϵʱ��OA+OB+OC����Сֵ������ͼ2�л�������������ͼ�Σ���˵�����ɣ�
�����ȱߡ�ABC�ı߳�Ϊ1��ֱ��д��OA+OB+OC����Сֵ��
���𰸡�
��1��
�⣺�١�AOB=150�㣬��BOC=120�㣬
���AOC=360�㩁120�㩁150��=90�㣬
�߽���BOC�Ƶ�C��˳ʱ�뷽����ת60��á�ADC��
���OCD=60�㣬��D=��BOC=120�㣬
���DAO=360�㩁��AOC����OCD����D=90�㣬
�ʴ�Ϊ��90�㣻
���߶�OA��OB��OC֮���������ϵ��OA2+OB2=OC2��
��ͼ1������OD��
�ߡ�BOC�Ƶ�C��˳ʱ�뷽����ת60��á�ADC��
���ADC�ա�BOC����OCD=60�㣬
��CD=OC����ADC=��BOC=120�㣬AD=OB��
���OCD�ǵȱ������Σ�
��OC=OD=CD����COD=��CDO=60�㣬
�ߡ�AOB=150�㣬��BOC=120�㣬
���AOC=90�㣬
���AOD=30�㣬��ADO=60�㣬
���DAO=90�㣬
��Rt��ADO�У���DAO=90�㣬
��OA2+OB2=OD2��
��OA2+OB2=OC2
��2��
�⣺�ٵ���=��=120��ʱ��OA+OB+OC����Сֵ��
��ͼ2������AOC�Ƶ�C��˳ʱ�뷽����ת60��á�A��O��C������OO�䣬
���A��O��C�ա�AOC����OCO��=��ACA��=60�㣬
��O��C=OC��O��A��=OA��A��C=BC��
��A��O��C=��AOC��
���OC O���ǵȱ������Σ�
��OC=O��C=OO�䣬��COO��=��CO��O=60�㣬
�ߡ�AOB=��BOC=120�㣬
���AOC=��A��O��C=120�㣬
���BOO��=��OO��A��=180�㣬
���ĵ�B��O��O�䣬A�乲�ߣ�
��OA+OB+OC=O��A��+OB+OO��=BA��ʱֵ��С��
�ڡߡ�AOB=��BOC=120�㣬
���AOC=120�㣬
��OΪ��ABC�����ģ�
���ĵ�B��O��O�䣬A�乲�ߣ�
��BD��AC��
�߽���AOC�Ƶ�C��˳ʱ�뷽����ת60��á�A��O��C��
��A��C=AC=BC��
��A��B=2BD��
��Rt��BCD��BD= ![]() BC=
BC= ![]() ��
��
��A��B= ![]() ��
��
�൱�ȱߡ�ABC�ı߳�Ϊ1ʱ��OA+OB+OC����СֵA��B= ![]() ��
��

����������1���ٸ����ܽǵĶ���õ���AOC=360�㩁120�㩁150��=90�㣬���ڽ���BOC�Ƶ�C��˳ʱ�뷽����ת60��á�ADC�����ǵõ���OCD=60�㣬��D=��BOC=120�㣬�����ı��ε��ڽǺͼ��ɵõ����ۣ�����ͼ1������OD�����ڡ�BOC�Ƶ�C��˳ʱ�뷽����ת60��á�ADC���õ���ADC�ա�BOC����OCD=60�㣬����ȫ�������ε����ʵõ�CD=OC����ADC=��BOC=120�㣬AD=OB���Ƴ���OCD�ǵȱ������Σ����ݵȱ������ε����ʵõ�OC=OD=CD����COD=��CDO=60�㣬���ڡ�AOB=150�㣬��BOC=120�㣬�õ���AOC=90�㣬��á�AOD=30�㣬��ADO=60�㣬���ݹ��ɶ������ɵõ����ۣ���2������ͼ2������ת�����ʵõ�O��C=OC��O��A��=OA��A��C=BC����A��O��C=��AOC�����Ƴ���OC O���ǵȱ������Σ����ݵȱ������ε����ʵõ�OC=O��C=OO�䣬��COO��=��CO��O=60�㣬���ڡ�AOB=��BOC=120�㣬�õ���AOC=��A��O��C=120�㣬�Ƴ��ĵ�B��O��O�䣬A�乲�ߣ����ɵõ����ۣ��ڸ��ݢٵĽ��ۼ��ɵõ������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������A��B��Ӧ�����ֱ�Ϊ��1��3����PΪ������һ���㣮
��1������P����A����B�ľ�����ȣ�д����P��Ӧ������ ����
��2������P����A��B�ľ���֮��Ϊ6����ô��P��Ӧ������ ����
��3����A��B�ֱ���2����λ����/�֡�1����λ����/�ֵ��ٶ������˶���ͬʱP����6����λ����/�ֵ��ٶȴ�O�������˶���������Aʱ����P������ͬ�����ٶ������˶�������ͣ�������ڵ�A���B֮�䣬��A���B�غ�ʱ����P����������·���Ƕ��٣�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶�����࣬��ѡ��![]() ��ѧ���μ�ѧУ���е���������д������Ԥ����������ѡ�ֵijɼ����£�
��ѧ���μ�ѧУ���е���������д������Ԥ����������ѡ�ֵijɼ����£�
![]() �ࣺ
�ࣺ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
![]() �ࣺ
�ࣺ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
ͨ���������õ����ݷ��������£�
�༶ | ��߷� | ƽ���� | ��λ�� | ���� | ���� |
|
|
|
|
|
|
|
|
|
|
|
|
![]() ֱ��д������
ֱ��д������![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
![]() �������ݷ�����������˵������߷���
�������ݷ�����������˵������߷���![]() �࣬
�࣬![]() ��ijɼ���
��ijɼ���![]() ���������Ҳ����˵
���������Ҳ����˵![]() ��ijɼ�Ҫ�ã����������֧��
��ijɼ�Ҫ�ã����������֧��![]() ��ɼ��õ����ɣ�
��ɼ��õ����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������A���ʾ��a��B��ʾ��b��C���ʾ��c��b����С������������a��b����![]() +(c��7)2=0��
+(c��7)2=0��
(1) a= ��b= ��c= ��
(2) ���������۵���ʹ��A����C���غϣ����B���� ��ʾ�ĵ��غϣ�
(3) ��A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�4����λ���ȵ��ٶ������˶�������t���ӹ�������A���B֮��ľ����ʾΪAB����A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC����AB= ��AC= ��BC= ��(�ú�t�Ĵ���ʽ��ʾ)
(4) ���ʣ�3BC��2AB��ֵ�Ƿ�����ʱ��t�ı仯���ı�? ���仯����˵�����ɣ������䣬������ֵ��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ҫ���������⣮
�벹ȫ������ʽ��2x2��4x��0�Ľ⼯�Ĺ��̣�
�ٹ��캯��������ͼ���ݲ���ʽ����������κ���y=��2x2��4x���������������ϵ�У�ͼ1���������κ���y=��2x2��4x��ͼ��ֻ����ͼ�ɣ���
����ý�㣬��ʾ���裬��y=0ʱ����÷��̩�2x2��4x=0�Ľ�Ϊ���٣������þ���߱�ʾ������y=��2x2��4xͼ����y��0�IJ��֣�
�۽���ͼ��д���⼯��������ʾͼ�ɵò���ʽ��2x2��4x��0�Ľ⼯Ϊ��2��x��0����������������һԪһ�β���ʽ�⼯�Ĺ��̣���ʽx2��2x+1��4�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AB=AC����D�ڱ�BC���ڵ�ֱ���ϣ�����D��DF��AC��ֱ��AB�ڵ�F��DE��AB��ֱ��AC�ڵ�E��
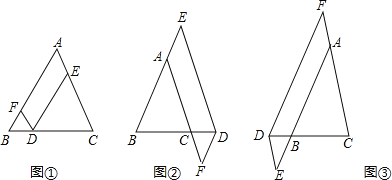
��1������D�ڱ�BC��ʱ����ͼ������֤��DE+DF=AC��
��2������D�ڱ�BC���ӳ�����ʱ����ͼ��������D�ڱ�BC�ķ����ӳ�����ʱ����ͼ������ֱ�д��ͼ����ͼ����DE��DF��AC֮���������ϵ������Ҫ֤����
��3����AC=6��DE=4����DF=�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ͬѧ�ǿ����Ķ�������ij��ѧͼ�����������ʹ�����ϵ��ͼ�飬ÿ���鵥��Ϊ16Ԫ����ļ�Ǯ���ʷ���ͨ���ʾֻ���ص�����ۿۡ��ʷѺͻ��Ļ�����±���ʾ���ܷ���=�����+���ʷ�+�ܻ�ѣ�
�������� | �ۿ� | �ʷ� | ��� |
������10�� | ���� | 6Ԫ | ÿ100Ԫ�������1Ԫ ������100Ԫʱ��100Ԫ����ջ�ѣ� |
����10�� | ���� | ����۵�10% | ÿ100Ԫ�������1Ԫ ������100Ԫ�IJ��ֲ��ջ�ѣ� |
��1����һ���ʹ�7���������ܷ���Ϊ�� ��Ԫ��
��2����֪ѧУͼ����蹺ͼ���������10�����������ҳ���10����
�����ִ��ʹ����ֱ��ÿ���ʹ�10�����ܷ���Ϊ1064Ԫʱ�����ʹ��˶౾ͼ�飿
��������ѧУͼ��ݸ����ˣ��ӽ�Լ�ĽǶȳ���������ÿ���ʹ�10��������һ�����ʹ��������ַ�ʽ��ѡ��һ�֣����ѡ����һ�֣����㲢˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ACB��90�㣬AC��BC����C(1��2)��A(��2��0)�����B��������__________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ȱ���ABC�ı߳�Ϊ4cm����P��Q�ֱ��B��C����ͬʱ���������е�P��BC���յ�C�˶����ٶ�Ϊ1cm/s��
��Q��CA��AB���յ�B�˶����ٶ�Ϊ2cm/s���������˶���ʱ��Ϊx��s����
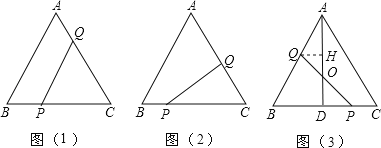
��1����ͼ��1������xΪ��ֵʱ��PQ��AB��
��2����ͼ��2������PQ��AC����x��
��3����ͼ��3��������Q��AB���˶�ʱ��PQ����ABC�ĸ�AD���ڵ�O��OQ��OP�Ƿ�������ȣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com