
【题目】已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;
点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s),
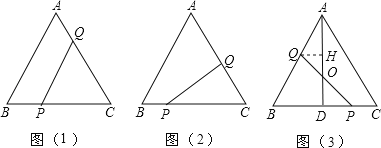
(1)如图(1),当x为何值时,PQ∥AB;
(2)如图(2),若PQ⊥AC,求x;
(3)如图(3),当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
【答案】(1)当x=![]() 时,PQ∥AB;(2)x=
时,PQ∥AB;(2)x=![]() ;(3)见解析
;(3)见解析
【解析】
试题(1)首先得出△PQC为等边三角形,进而表示出PC=4﹣x,CQ=2x,由4﹣x=2x,求出答案;
(2)根据题意得出CQ=![]() PC,即2x=
PC,即2x=![]() (4﹣x),求出即可;
(4﹣x),求出即可;
(3)根据题意得出QH=DP,进而判断出△OQH≌△OPD(AAS),即可得出答案.
解:(1)∵∠C=60°,
∴当PC=CQ时,△PQC为等边三角形,
于是∠QPC=60°=∠B,
从而PQ∥AB,
∵PC=4﹣x,CQ=2x,
由4﹣x=2x,
解得:x=![]() ,
,
∴当x=![]() 时,PQ∥AB;
时,PQ∥AB;
(2)∵PQ⊥AC,∠C=60°,
∴∠QPC=30°,
∴CQ=![]() PC,
PC,
即2x=![]() (4﹣x),
(4﹣x),
解得:x=![]() ;
;
(3)OQ=PO,理由如下:
作QH⊥AD于H,如图(3),
∵AD⊥BC,
∴∠QAH=30°,BD=![]() BC=2,
BC=2,
∴QH=![]() AQ=
AQ=![]() (2x﹣4)=x﹣2,
(2x﹣4)=x﹣2,
∵DP=BP﹣BD=x﹣2,
∴QH=DP,
在△OQH和△OPD中,
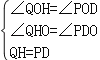 ,
,
∴△OQH≌△OPD(AAS),
∴OQ=OP.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】已知,点O是等边△ABC内的任一点,连接OA,OB,OC.
(1)如图1,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①∠DAO的度数是多少?
②用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)设∠AOB=α,∠BOC=β.
①当α,β满足什么关系时,OA+OB+OC有最小值?请在图2中画出符合条件的图形,并说明理由;
②若等边△ABC的边长为1,直接写出OA+OB+OC的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张长方形纸片,剪下一个正方形,剩下一个长方形,称为第一次操作;在剩下的长方形纸片中再剪下一个正方形,剩下一个长方形,称为第二次操作;…;若在第n次操作后,剩下的长方形为正方形,则称原长方形为n阶奇异长方形.如图1,长方形ABCD中,若AB=2,BC=6,则称长方形ABCD为2阶奇异长方形.

(1)判断与操作:如图2,长方形ABCD长为10,宽为6,它是奇异长方形,请写出它是____阶奇异长方
形,并在图中画出裁剪线;
探究与计算:已知长方形ABCD的一边长为24,另一边长为a (a<24),且它是3阶奇异长方形,请画出所
有可能的长方形ABCD及裁剪线的示意图,并求出相应的a值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求 ![]() 的值.
的值.
(1)小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
请回答: ![]() 的值为 .
的值为 .
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3.
①求 ![]() 的值;
的值;
(3)②若CD=2,则BP= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角△ABC中,∠BAC=90°,AB=AC=2,点E是BC边上一点,∠DEF=45°且角的两边分别与边AB,射线CA交于点P,Q.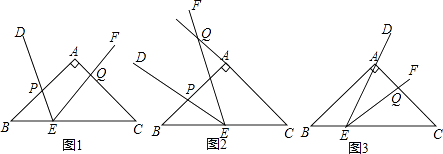
(1)如图2,若点E为BC中点,将∠DEF绕着点E逆时针旋转,DE与边AB交于点P,EF与CA的延长线交于点Q.设BP为x,CQ为y,试求y与x的函数关系式,并写出自变量x的取值范围;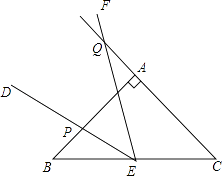
(2)如图3,点E在边BC上沿B到C的方向运动(不与B,C重合),且DE始终经过点A,EF与边AC交于Q点.探究:在∠DEF运动过程中,△AEQ能否构成等腰三角形,若能,求出BE的长;若不能,请说明理由.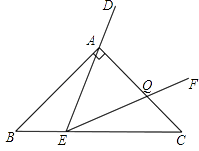
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )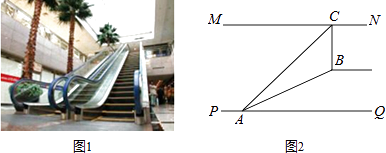
A.10.8米
B.8.9米
C.8.0米
D.5.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
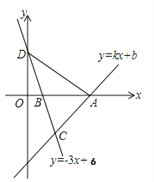
【题目】如图,一次函数y=kx+b的图象经过点A(8,0),直线y=-3x+6与x轴交于点B,与y轴交于点D,且两直线交于点C(4,m).
(1)求m的值及一次函数的解析式;
(2)求△ACD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,七(2)班的张明、王强等同学随家长一同到某公园游玩,下面是购买门票时,张明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
⑴张明他们一共去了几个成人,几个学生?
⑵请你帮助张明算一算,用哪种方式购票(团体购票还是非团体购票)更省钱?说明理由.
⑶正要购票时,张明发现七(3)班的张小毛等15名同学和他们的2名家长共17人也来购票,请你为他们设计出最省的购票方案,并求出此时的购票费用.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com