
【题目】暑假期间,七(2)班的张明、王强等同学随家长一同到某公园游玩,下面是购买门票时,张明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
⑴张明他们一共去了几个成人,几个学生?
⑵请你帮助张明算一算,用哪种方式购票(团体购票还是非团体购票)更省钱?说明理由.
⑶正要购票时,张明发现七(3)班的张小毛等15名同学和他们的2名家长共17人也来购票,请你为他们设计出最省的购票方案,并求出此时的购票费用.

【答案】(1)学生人数为12-8=4人,成人人数为8人.(2)购团体票更省钱.(3)最省的购票方案为:买16人的团体票,再买13张学生票;644元.
【解析】
(1)设去了x个成人,则去了(12-x)个学生,根据等量关系:成人的票价+学生的票价=400元,据此列方程求解.
(2)计算团体票所需费用,和400元比较即可求解.
(3)根据(2)可得出购票省钱的方案,运用到本问得求解中来即可.
解:(1)设成人人数为x人,则学生人数为(12-x)人,则:
由题中所给的票价单可得:40x+ 20×(12-x)=400
解得:x=8
答:学生人数为12-8=4人,成人人数为8人.
(2)如果买团体票,按16人计算,共需费用:
40×0.6×16=384元.
384<400
所以,购团体票更省钱.
(3)最省的购票方案为:买16人的团体票,再买13张学生票.
此时的购票费用为:
16×40×0.6+13×20=644元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;
点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s),
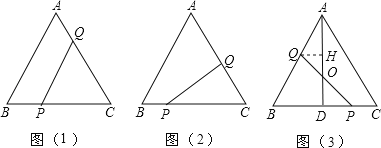
(1)如图(1),当x为何值时,PQ∥AB;
(2)如图(2),若PQ⊥AC,求x;
(3)如图(3),当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
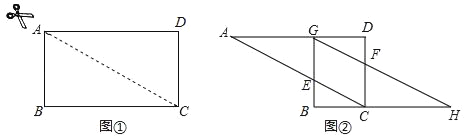
【题目】如图①,将一个长方形沿着对角线剪开即可得到两个全等的三角形,再把△ABC沿着AC方向平移,得到图②中的△GBH,BG交AC于点E,GH交CD于点F.在图②中,除△ACD与△HGB全等外,你还可以指出哪几对全等的三角形(不能添加辅助线和字母)?请选择其中一对加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售“喜羊羊”玩具,预测该产品能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,商场又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个进价多了10元.
(1)该商场两次共购进这种玩具多少个?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每件售价至少是多少元?(利润率![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
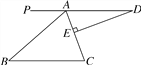
【题目】如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.
(1)求∠B的度数,并判断△ABC的形状;
(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
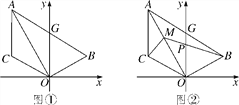
【题目】如图①,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴于G,连接OB,OC.
(1)判断△AOG的形状,并予以证明;
(2)若点B,C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图②,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OA交圆O于点F,则∠CBF等于( ) 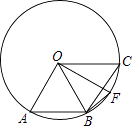
A.12.5°
B.15°
C.20°
D.22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设三角形三个内角的度数分别为x,y,z,如果其中一个角的度数是另一个角的度数的2倍,那么我们称数对(y,z)(y≤z)是x的和谐数对.例:当x=150°时,对应的和谐数对有一个,它为(10,20);当x=66时,对应的和谐数对有二个,它们为(33,81),(38,76).当对应的和谐数对(y,z)有三个时,此时x的取值范围是____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com