
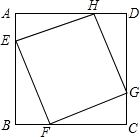
已知:如图,正方形ABCD的边长为1,点E,F,G,H分别在AB,BC,CD,DA上,且四边形EFGH也是正方形,设AE=x,正方形EFGH的面积为S.
(1)求证:△AEH≌△BFE;
(2)求S与x之间的函数关系式.
【考点】全等三角形的判定与性质;根据实际问题列二次函数关系式;正方形的性质.
【分析】(1)利用正方形的性质,用AAS证明△AEH≌△BFE;
(2)利用△AEH≌△BFE,得到BF=AE=x,利用勾股定理,在Rt△BFE中,EF2=BF2+BE2=x2+(1﹣x)2,所以S=EF2=x2+(1﹣x)2=2x2﹣2x+1.
【解答】解:(1)∵四边形ABCD为正方形,四边形EFGH也是正方形,
∴∠A=∠B=∠HEF=90°,EH=FE,
∴∠AEH+∠AHE=90°,∠AEH+∠BEF=90°,
∴∠AHE=∠BEF,
在△AEH和△BFE中,
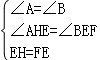 ,
,
∴△AEH≌△BFE.
(2)∵△AEH≌△BFE,
∴BF=AE=x,(0<x<1)
在Rt△BFE中,EF2=BF2+BE2=x2+(1﹣x)2,
∴S=EF2=x2+ (1﹣x)2=2x2﹣2x+1,(0<x<1)
(1﹣x)2=2x2﹣2x+1,(0<x<1)
【点评】本题考查了正方形的性质、全等三角形的性质与判定,解决本题的关键是证明)△AEH≌△BFE.


科目:初中数学 来源: 题型:
为了估算湖里有多少条鱼,从湖里捕上100条做上标记,然后放回湖里,经过一段时间待标记的鱼全混合于鱼群中后,第二次捕得200条,发现其中带标记的鱼25条,我们可以估算湖里有鱼__________条.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线y=ax2+b(a≠0)在平面直角坐标系中的位置如图所示,那么一元二次方程ax2﹣x+b=0根的情况是( )
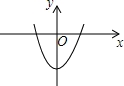
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法判断
查看答案和解析>>
科目:初中数学 来源: 题型:
在纸上剪下一个圆和一个扇形纸片,使它们恰好围成一个圆锥(如图所示),如果扇形的圆心角为90°,扇形的半径为16,那么所围成的圆锥的高为__________.
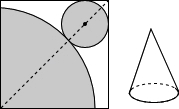
查看答案和解析>>
科目:初中数学 来源: 题型:
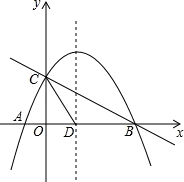
如图,直线y1=﹣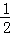 x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).
x+2与x轴,y轴分别交于B,C,抛物线y=ax2+bx+c(a≠0)经过点A,B,C,点A坐标为(﹣1,0).
(1)求抛物线的解析式;
(2)抛物线的对称轴与x轴交于点D,连接CD,点P是直线BC上方抛物线上的一动点(不与B,C重合),当点P运动到何处时,四边形PCDB的面积最大?求出此时四边形PCDB面积的最大值和点P坐标;
(3)在抛物线上的对称轴上是否存在一点Q,使△QCD是以CD为腰的等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com