练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    等腰三角形的两边长分别是3和7，则其周长为__________．


    17．

    【考点】等腰三角形的性质．

    【专题】分类讨论．

    【分析】因为边为3和7，没明确是底边还是腰，所以有两种情况，需要分类讨论．

    【解答】解：分两种情况：

    当3为底时，其它两边都为7，3、7、7可以构成三角形，周长为17；

    当3为腰时，其它两边为3和7，3+3=6＜7，所以不能构成三角形，故舍去，

    所以等腰三角形的周长为17．

    故答案为：17．

    【点评】本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


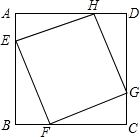
    已知：如图，正方形ABCD的边长为1，点E，F，G，H分别在AB，BC，CD，DA上，且四边形EFGH也是正方形，设AE=x，正方形EFGH的面积为S．

    （1）求证：△AEH≌△BFE；

    （2）求S与x之间的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    三角形的外角和等于__________度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    数学课上，探讨角平分线的作法时，徐老师用直尺和圆规作角平分线，方法如下：

    作法：①如图①，在射线OA、OB上，分别截取OD、OE，使OD=OE；

    ②分别以点D和点E为圆心，适当长（大于线段DE长的一半）为半径作圆弧，在∠AOB的内部，两弧交于点C；

    ③作射线OC．

    徐老师又介绍用角尺平分一个任意角的方法，作法如下：

    如图②，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与点M，N重合，过角尺顶点C的射线OC便是∠AOB的平分线．

    （1）徐老师用尺规作图作角平分线时，用到的三角形全等的判定方法是__________；

    （2）请证明徐老师用角尺平分一个任意角的方法．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若x+y=3且xy=1，则代数式（2﹣x）（2﹣y）的值等于(     )

    A．2       B．1       C．0       D．﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算：．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


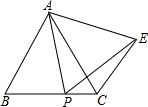
    如图，△ABC是等边三角形，P为BC上一动点（不与B、C重合），以AP为边作等边△APE，连接CE．

    （1）求证：AB∥CE；

    （2）是否存在点P，使得AE⊥CE？若存在，指出点P的位置并证明你的结论；若不存，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知圆锥的高是4cm，底面半径是3cm，则圆锥的表面积是　　　　　　cm2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在一个不透明的布袋中，红色、黑色、白色的玻璃球共有40个，除颜色外其他完全相同．小张通过多次摸球试验后发现，其中摸到红色、黑色球的频率稳定在15%和45%，则口袋中白色球的个数很可能是（　　）

    A．6    B．16   C．18   D．24

    查看答案和解析>>

    同步练习册答案