
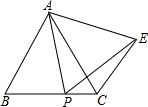
如图,△ABC是等边三角形,P为BC上一动点(不与B、C重合),以AP为边作等边△APE,连接CE.
(1)求证:AB∥CE;
(2)是否存在点P,使得AE⊥CE?若存在,指出点P的位置并证明你的结论;若不存,请说明理由.

【考点】全等三角 形的判定与性质;等边三角形的性质.
形的判定与性质;等边三角形的性质.
【分析】(1)根据等边三角形的性质得出角相等、边相等,证出△A BP≌△ACE(SAS),得出对应角相等,证出∠BAC=∠ACF,从而证出结论.
BP≌△ACE(SAS),得出对应角相等,证出∠BAC=∠ACF,从而证出结论.
(2)由△ABP≌△ACE得出∠APB=∠AEC=90°,再由等边三角形的性质得出P为BC的中点.
【解答】证明:(1)∵△ABC、△APE是等边三角形,
∴∠BAC=∠PAE=∠B=60°,AB=AC,AF=AE,
∴∠BAP=∠CAE,
在△ABF和△ACE中,
∴△ABP≌△ACE(SAS),
∴∠B=∠ACP=60°,
∴∠BAC=∠ACF,
∴AB∥CE;
(2)存在点P使得AE⊥CE.此时P为BC的中点;理由如下:
∵AE⊥CE,
∴∠AEC=90°,
由(1)得:△ABP≌△A CE,
CE,
∴∠APB=∠AEC=90°,
∴AP⊥BC,
∵AB=AC,
∴P为BC的中点.
∴存在点P,使得AE⊥CE.
【点评】本题考查了等边三角形的性质以及全等三角形的判定与性质;由等边三角形证明三角形全等是关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
如图,在6×10的正方形网格中,每个小正方形的边长均为1,每个小正方形顶点叫做格点,△ABC的三个顶点 和点D、E、F、G、H、K均在格点上,现以D、E、F、G、H、K中的三个点为顶点画三角形.
和点D、E、F、G、H、K均在格点上,现以D、E、F、G、H、K中的三个点为顶点画三角形.
(1)在图①中画出一个三角形与△ABC全等;
(2)在图②中画出一个三角形与△ABC面积相等但不全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
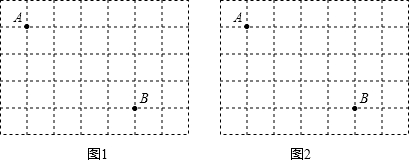
图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A和点B在小正方形的顶点上.
(1)在图1中画出△ABC(点C在小正方形的顶点上),使△ABC为直角三角形(画一个即可);
(2)在图2中画出△ABD(点D在小正方形的顶点上),使△ABD为等腰三角形(画一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点O,与D1E1相交于点F.
(1)求∠OFE1的度数;
(2)求线段AD1的长;
(3)若把三角形D1CE1绕着点C顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部,外部,还是边上?证明你的判断.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com