练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若x+y=3且xy=1，则代数式（2﹣x）（2﹣y）的值等于(     )

    A．2       B．1       C．0       D．﹣1


    D【考点】整式的混合运算—化简求值．

    【分析】先算乘法，再变形，最后整体代入求出即可．

    【解答】解：∵x+y=3，xy=1，

    ∴（2﹣x）（2﹣y）

    =4﹣2y﹣2x+xy

    =4﹣2（x+y）+xy

    =4﹣2×3+1

    =﹣1，

    故选D．

    【点评】本题考查了整式的混合运算和求值的应用，能正确运用整式的运算法则进行化简是解此题的关键，用了整体代入得思想，难度适中．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


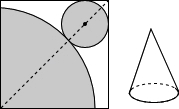
    在纸上剪下一个圆和一个扇形纸片，使它们恰好围成一个圆锥（如图所示），如果扇形的圆心角为90°，扇形的半径为16，那么所围成的圆锥的高为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个多边形的内角和是1260°，这个多边形的边数是(     )

    A．7       B．8       C．9       D．10

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在6×10的正方形网格中，每个小正方形的边长均为1，每个小正方形顶点叫做格点，△ABC的三个顶点和点D、E、F、G、H、K均在格点上，现以D、E、F、G、H、K中的三个点为顶点画三角形．

    （1）在图①中画出一个三角形与△ABC全等；

    （2）在图②中画出一个三角形与△ABC面积相等但不全等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    探究：中华人民共和国国旗上的五角星的每个角均相等，小明为了计算每个角的度数，画出了如图①的五角星，每个角均相等，并写出了如下不完整的计算过程，请你将过程补充完整．

    解：∵∠AFG=∠C+∠E，∠AGF=∠B+∠D．

    ∴∠AFG+∠AGF=∠C+∠E+∠B+∠D．

    ∵∠A+∠AFG+∠AGF=__________°，

    ∴∠A+∠B+∠C+∠D+∠E=__________°，

    ∴∠A=∠B=∠C=∠D=∠E=__________°．

    拓展：如图②，小明改变了这个五角星的五个角的度数，使它们均不相等，请你帮助小明求∠A、∠B、∠C、∠D、∠E的和．

    应用：如图③．小明将图②中的点A落在BE上，点C落在BD上，若∠B=∠D=36°，则∠CAD+∠ACE+∠E=__________°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    等腰三角形的两边长分别是3和7，则其周长为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


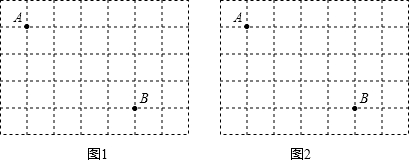
    图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，点A和点B在小正方形的顶点上．

    （1）在图1中画出△ABC（点C在小正方形的顶点上），使△ABC为直角三角形（画一个即可）；

    （2）在图2中画出△ABD（点D在小正方形的顶点上），使△ABD为等腰三角形（画一个即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直线AB与半径为2的⊙O相切于点C，D是⊙O上一点，且∠EDC=30°，弦EF∥AB，则EF的长度为（　　）

    A．2    B．2 C．  D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，已知在平行四边形ABCD中，AB＝5，BC＝8，cosB＝，点P是边BC上的动点，以CP为半径的圆C与边AD交于点E、F（点F在点E的右侧），射线CE与射线BA交于点G．

    （1）当圆C经过点A时，求CP的长；

    （2）连结AP，当AP//CE时，求弦EF的长；

    （3）当△AGE是等腰三角形时，求圆C的半径长．

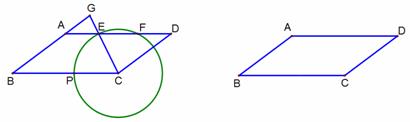
    图1                           备用图

    查看答案和解析>>

    同步练习册答案