
如图1,已知在平行四边形ABCD中,AB=5,BC=8,cosB= ,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.
,点P是边BC上的动点,以CP为半径的圆C与边AD交于点E、F(点F在点E的右侧),射线CE与射线BA交于点G.
(1)当圆C经过点A时,求CP的长;
(2)连结AP,当AP//CE时,求弦EF的长;
(3)当△AGE是等腰三角形时,求圆C的半径长.
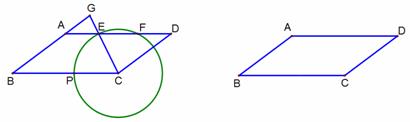
图1 备用图
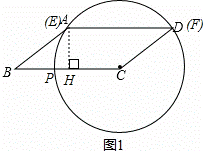 (1)如图1,设⊙O的半径为r,
(1)如图1,设⊙O的半径为r,
当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,
∴BH=AB 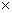 cosB=4,
cosB=4,
∴AH=3,CH=4,············1分
∴AC=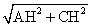 ==5,
==5,
∴此时CP=r=5;···············2分
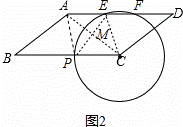 (2)如图2,若AP∥CE,APCE为平行四边形,
(2)如图2,若AP∥CE,APCE为平行四边形,
∵CE=CP,
∴四边形APCE是菱形,···········3分
连接AC、EP,则AC⊥EP,
∴AM=CM= 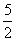 ,·········4分
,·········4分
由(1)知,AB=AC,则∠ACB=∠B,
∴CP=CE= 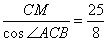 ,··········5分
,··········5分
∴EF=2 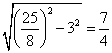 ···········6分
···········6分
(3)如图3:过点C作CN⊥AD于点N,过点A作AQ⊥BC于点Q,
∵cosB= 
∴∠B<45°,············7分
∵∠BCG<90°,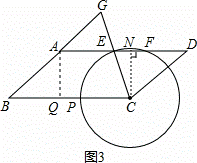
∴∠BGC>45°,············8分
∴∠BGC>∠B=∠GAE,即∠BGC≠∠GAE,
又∠AEG=∠BCG≥∠ACB=∠B=∠GAE,
∴当∠AEG=∠GAE时,A、E、G重合,则△AGE不存在.
即∠AEG≠∠GAE
∴只能∠AGE=∠AEG,············10分
∵AD∥BC,
∴△GAE∽△GBC,
∴ 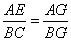 ··············11分
··············11分
即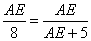 ······················12分
······················12分
解得,AE=3,EN=AN-AE=1
∴CE=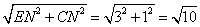 ················13分
················13分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,在△ABC中,先作∠BAC的角平分线AD交BC于点D,再以AC边上的一点O为圆心,过A、D两点作⊙O(用尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
查看答案和解析>>
科目:初中数学 来源: 题型:
已知直线y=kx(k>0)与双曲线y=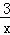 交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为( )
交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为( )
A.-6 B.-9 C.0 D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
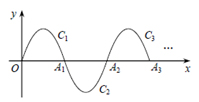
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;……
如此进行下去,直至得C13.若点P(37,m)
在第13段抛物线C13上,则m = .
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同.小张通过多次摸球试验后发现,其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是( )
A.6 B.16 C.18 D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若AB=8cm,BC=10cm,求大圆与小圆围成的圆环的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是……………………………………………………………( )
A.y=2x+3 B.y=x﹣3 C.y=2x﹣3 D.y=﹣x+3
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com