练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，∠B=45°，∠D=64°，AC=BC，则∠E的度数是（　　）

    A．45°   B．26°    C．36°   D．64°


    B【考点】等腰三角形的性质；三角形内角和定理．

    【分析】由在△ABC中，∠B=45°，AC=BC，根据等腰三角形的性质，即可求得∠A的度数，继而求得∠ECD的度数，继而求得答案．

    【解答】解：∵在△ABC中，∠B=45°，AC=BC，

    ∴∠A=∠B=45°，

    ∴∠DCE=∠ACB=180°﹣∠A﹣∠B=90°，

    ∵∠D=64°，

    ∴∠E=90°﹣∠D=26°．

    故选B．

    【点评】此题考查了等腰三角形的性质以及三角形内角和定理．注意根据等腰三角形的性质求得∠ACB=90°是关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


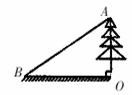
    如图，为测量一棵与地面垂直的树OA的高度，在距离树的底端O点30米的B处，测得

    树顶4的仰角∠ABO为α，则树OA的高度为

      A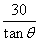．米    B．30sinα米    C．30tanα米    D．30cosα米

    查看答案和解析>>

    科目：初中数学 来源： 题型：


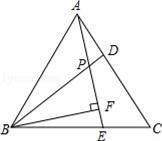
    如图，已知△ABC是等边三角形，D、E分别是AC、BC上的两点，AD=CE，且AE与BD交于点P，BF⊥AE于点F．

    （1）求证：△ABD≌△CAE；

    （2）若BP=6，求PF的长．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某次射击训练中，一小组的成绩如下表所示．若该小组的平均成绩为7.7环，则成绩为8环的人数是　　　　　　．

    环数

    6

    7

    8

    9

    人数

    1

    3

     

    2

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AC，交AB于E，若AB=5，求线段DE的长．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分式方程的解是（　　）

    A．x=﹣1      B．x=  C．x=﹣3      D．x=

    查看答案和解析>>

    科目：初中数学 来源： 题型：


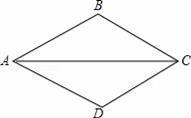
    如图，已知△ABC，按如下步骤作图：①以A为圆心，AB长为半径画弧；②以C为圆心，CB长为半径画弧，两弧相交于点D；③连结AD，CD．则△ABC≌△ADC的依据是　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列计算正确的是(   )

     A. 92=18      B. －22=4        C. 2×(－2)=(－2)     D. 22＋22=2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


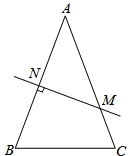
    如图，在△ABC中，AB=AC，AB的垂直平分线交AB于N，交AC于M．

    （1）若∠B=70°，则∠NMA的度数是__________；

    （2）探究∠B与∠NMA的关系，并说明理由；

    （3）连接MB，若AB=8cm，△MBC的周长是14cm．

    ①求BC的长；

    ②在直线MN上是否存在点P，使PB+CP的值最小？若存在，标出点P的位置并求PB+CP的最小值；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案