Question

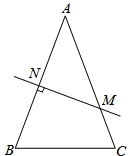
如图，在△ABC中，AB=AC，AB的垂直平分线交AB于N，交AC于M．

（1）若∠B=70°，则∠NMA的度数是__________；

（2）探究∠B与∠NMA的关系，并说明理由；

（3）连接MB，若AB=8cm，△MBC的周长是14cm．

①求BC的长；

②在直线MN上是否存在点P，使PB+CP的值最小？若存在，标出点P的位置并求PB+CP的最小值；若不存在，说明理由．

Answer 1

【考点】轴对称-最短路线问题；线段垂直平分线的性质；等腰三角形的性质．

【分析】（1）根据等腰三角的性质，三角形的内角和定理，可得∠A的度数，根据直角三角形两锐角的关系，可得答案；

（2）根据等腰三角的性质，三角形的内角和定理，可得∠A的度数，根据直角三角形两锐角的关系，可得答案；

（3）根据垂直平分线的性质，可得AM与MB的关系，再根据三角形的周长，可得答案；根据两点之间线段最短，可得P点与M点的关系，可得PB+PC与AC的关系．

【解答】解：（1）若∠B=70°，则∠NMA的度数是 50°，

故答案为：50°；

（2）猜想的结论为：∠NMA=2∠B﹣90°．

理由：∵AB=AC，

∴∠B=∠C，

∴∠A=180°﹣2∠B，

又∵MN垂直平分AB，

∴∠NMA=90°﹣∠A=90°﹣（180°﹣2∠B）=2∠B﹣90°．

（3）如图：

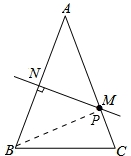
①∵MN垂直平分AB．

∴MB=MA，

又∵△MBC的周长是14cm，

∴AC+BC=14cm，

∴BC=6cm．

②当点P与点M重合时，PB+CP的值最小，最小值是8cm．

【点评】本题考查了轴对称，线段垂直平分线上的点到线段两端点的距离相等得出PB=PA．