
如图,已知△ABC是等边三角形,D、E分别是AC、BC上的两点,AD=CE,且AE与BD交于点P,BF⊥AE于点F.
(1)求证:△ABD≌△CAE;
(2)若BP=6,求PF的长.
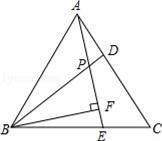

【考点】全等三角形的判定与性质;等边三角形的性质.
【分析】(1)由等边三角形的性质得出AB=CA,∠BAD=∠ACE=60°,由SAS即可证明△ABD≌△CAE;
(2)由△ABD≌△CAE得出对应角相等∠ABD=∠CAE,根据三角形的外角性质得出∠BPF=60°,由含30°角的直角三角形的性质即可得出PF的长.
【解答】(1)证明:∵△ABC是等边三角形,
∴AB=CA,∠BAD=∠ACE=60°,
在△ABD和△CAE中,
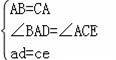
 ,
,
∴△ABD≌△CAE(SAS);
(2)解:∵△ABD≌△CAE,
∴∠ABD=∠CAE,
∵∠BPF=∠BAP+∠ABD,
∴∠BPF=∠BAP+∠CAE=∠BAD=60°,
∵BF⊥AE,
∴∠PFB=90°,
∴∠PBF=30°,
∴PF=
 BP=3.
BP=3.
【点评】本题考查了等边三角形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质;熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
为了市民出行更加方便,天津市政府大力发展公共交通,2013年天津市公共交通客运量约为1608000000人次,将1608000000用科学记数法表示为( )
A.160.8×107 B.16.08×108 C.1.608×109 D.0.1608×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
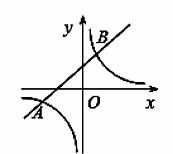
如图,已知一次函数与反比例函数的图象相交于A(-4,-2),B(a,4)两点.
(1)求反比例函数的表达式和点B的坐标;
(2)根据图象直接同答:当白变量x在什么范围时,一次函数的值大于反比例函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
某天,学校研究性学习小组的同学从8时起骑自行车外出调查,17时回到学校,小组离开学校的距离与时间的关系可用图中的曲线表示,根据这个曲线图,下列说法错误的是( )


A.在离校最远的地方调查的时间是14~15时
B.第一次调查从9时开始,历时2h
C.中午12~13时休息的地方离校15km
D.返校的速度最慢
查看答案和解析>>
科目:初中数学 来源: 题型:
下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为( )


A.50 B.64 C.68 D.72
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com