
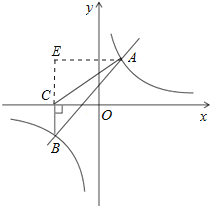
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点.
的图象相交于A(2,3),B(﹣3,n)两点.

(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
【答案】(1)y=![]() ,y=x+1;(2)﹣3<x<0或x>2;(3)5
,y=x+1;(2)﹣3<x<0或x>2;(3)5
【解析】
试题分析:(1)由一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,3),B(﹣3,n)两点,首先求得反比例函数的解析式,则可求得B点的坐标,然后利用待定系数法即可求得一次函数的解析式;
的图象相交于A(2,3),B(﹣3,n)两点,首先求得反比例函数的解析式,则可求得B点的坐标,然后利用待定系数法即可求得一次函数的解析式;
(2)根据图象,观察即可求得答案;
(3)因为以BC为底,则BC边上的高为3+2=5,所以利用三角形面积的求解方法即可求得答案.
解:(1)∵点A(2,3)在y=![]() 的图象上,
的图象上,
∴m=6,
∴反比例函数的解析式为:y=![]() ,
,
∵B(﹣3,n)在反比例函数图象上,
∴n=![]() =﹣2,
=﹣2,
∵A(2,3),B(﹣3,﹣2)两点在y=kx+b上,
∴![]() ,
,
解得:![]() ,
,
∴一次函数的解析式为:y=x+1;
(2)﹣3<x<0或x>2;
(3)以BC为底,则BC边上的高AE为3+2=5,
∴S△ABC=![]() ×2×5=5.
×2×5=5.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,G是CD上一点,延长BC到E,使CE=CG,连接BG并延长交DE于F.

(1)求证:△BCG≌△DCE;
(2)将△DCE绕点D顺时针旋转90°得到△DAE′,判断四边形E′BGD是什么特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)设方程两根为x1,x2是否存在实数a,使![]() ?若存在求出实数a,若不存在,请说明理由.
?若存在求出实数a,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
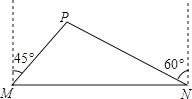
【题目】我市准备在相距2千米的M,N两工厂间修一条笔直的公路,但在M地北偏东45°方向、N地北偏西60°方向的P处,有一个半径为0.6千米的住宅小区(如图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
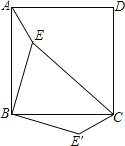
【题目】如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C= 度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com