
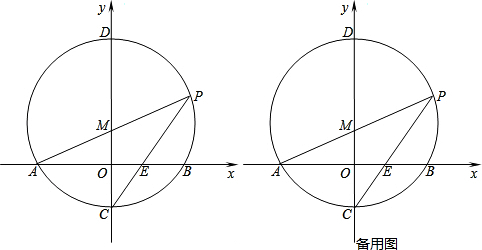
���� ��1������ֱ�������ε����ʿɵá�AMO=60�㣬��������ʿɵá�MCP=30�㣬��Բ�ܽǶ����ɵý��ۣ�
��2������Բ�ܽǶ����ʹ���������PB��MO��AO=BO���ɵ�PB=2OM����P�����꣬�ɵ�C�����꣬���ô���ϵ������ֱ��PC�Ľ���ʽ��
��3�������ν�Ͽɵ�S��MPF=S�ı���OMBP-S��MOF-S��PBF�����������ε������ʽ�����ε������ʽ���㼴�ɣ������öԳƵ����ʿɵõ���F�˶�����Eʱ����MPF���ܳ���С�����E������꣬�ɵá�MPF����С�ܳ���
��� �⣺��1����ֱ��������AMO�У�
��OM=$\frac{1}{2}$AM��
���MAO=30�㣬��AMO=60�㣬
��AM=MC��
��$��MPC=��MCP=\frac{1}{2}��AMO$=30�㣬
���PAO=��MCP��
��DP=BP������P��BD���е㣻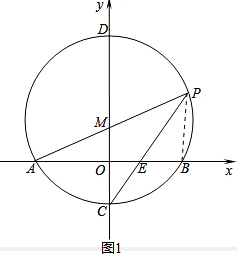
��2������BP����ͼ1��
��AP�ǡ�M��ֱ����
���PBA=90�㣬
��PC�ǡ�M��ֱ�����Ҵ�ֱ����AB��
��DCƽ����AB��
����Rt��AMO��AM=2$\sqrt{3}$��OM=$\sqrt{3}$��
��AO=OB=3��OC=MC-OM=2$\sqrt{3}-\sqrt{3}$=$\sqrt{3}$��
��C����������0��-$\sqrt{3}$����
��DC��AB��
��PB��MO��
��PB=2OM=2$\sqrt{3}$��
��P���������3��2$\sqrt{3}$����
�֡�C��0��-$\sqrt{3}$����
��ֱ��CP�Ľ���ʽΪy=kx+b��k��0���ã�$\left\{\begin{array}{l}{2\sqrt{3}=3k+b}\\{-\sqrt{3}=b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=-\sqrt{3}}\end{array}\right.$��
��ֱ��CP�Ľ���ʽΪ��y=$\sqrt{3}x-\sqrt{3}$��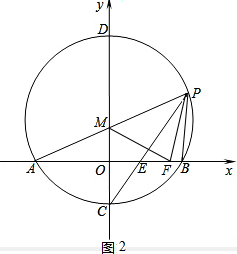
��3������ͼ2��S��MPF=S�ı���OMBP-S��MOF-S��PBF
=$\frac{1}{2}$����OM+BP����OB$-\frac{1}{2}OM•OF$$-\frac{1}{2}•BP•BF$
=$\frac{1}{2}$����$\sqrt{3}+2\sqrt{3}$����3$-\frac{\sqrt{3}}{2}$x-$\frac{2\sqrt{3}}{2}����3-x��$
=$\frac{\sqrt{3}}{2}x+\frac{3\sqrt{3}}{2}$��0��x��3����
�ڡߵ�M���C����AB�Գƣ�
�൱��F�˶�����Eʱ����MPF���ܳ���С��
��y=0����ֱ��CP�Ľ���ʽΪy=$\sqrt{3}x-\sqrt{3}$��
��ã�x=1��
���E��������1��0����
�൱��F������Ϊ��1��0��ʱ��ʹ��MPF���ܳ���С����MPF����С�ܳ�=PC+MP=6$+2\sqrt{3}$��
���� ������Ҫ�����˴���������ֱ�������ε����ʣ�Բ���й����ʺʹ���ϵ���������ʽ�ȣ��ۺ����ø��������ν���ǽ�����Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\frac{2}{3}$ | B�� | 3$\frac{1}{2}$ | C�� | 3$\frac{2}{3}$ | D�� | 4$\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
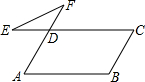 ��ͼ��ƽ���ı���ABCD�У���B=110�㣬�ӳ�CD��F���ӳ�AD��E������EF�����E+��F=70�㣮
��ͼ��ƽ���ı���ABCD�У���B=110�㣬�ӳ�CD��F���ӳ�AD��E������EF�����E+��F=70�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
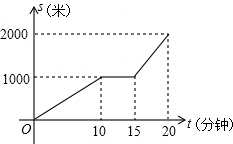 С��ij�������г���ѧ��;�������г��������ϣ���������һ��ʱ���������У���ʱ�ϵ���ѧУ������ѧʱ��ҵľ���s���ף������ʱ��t�����ӣ��ĺ���ͼ����ͼ��ʾ������˵���д�����ǣ�������
С��ij�������г���ѧ��;�������г��������ϣ���������һ��ʱ���������У���ʱ�ϵ���ѧУ������ѧʱ��ҵľ���s���ף������ʱ��t�����ӣ��ĺ���ͼ����ͼ��ʾ������˵���д�����ǣ�������| A�� | ��ʱ��Ϊ15���� | |
| B�� | ѧУ��ҵľ���Ϊ2000�� | |
| C�� | �Ӽҵ�ѧУ����ʱ��20���� | |
| D�� | ���г���������ʱ��Ҿ���Ϊ1000�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com