
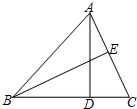
 如图,AD、BE分别是△ABC中BC、AC边上的高,BE=4,BC=6,则sin∠DAC=$\frac{\sqrt{5}}{3}$.
如图,AD、BE分别是△ABC中BC、AC边上的高,BE=4,BC=6,则sin∠DAC=$\frac{\sqrt{5}}{3}$. 分析 根据AD、BE分别是△ABC中BC、AC边上的高,可以求得∠EBC和∠DAC的关系,BE=4,BC=6,根据勾股定理可以求得CE的长,从而可以求出∠EBC的三角函数值,进而可以得到∠DAC的三角函数值,本题得以解决.
解答 解:∵AD、BE分别是△ABC中BC、AC边上的高,
∴∠BDA=∠ADC=90°,
∴∠CBE=∠DAC,
∵∠BEC=90°,BE=4,BC=6,
∴CE=2$\sqrt{5}$,
∴sin∠EBC=$\frac{\sqrt{5}}{3}$,
∴sin∠DAC=$\frac{\sqrt{5}}{3}$.
故答案为:$\frac{\sqrt{5}}{3}$.
点评 本题考查解直角三角形,解题的关键找出各个角之间的关系,利用等角的三角函数值相等,可以求得所求的角的三角函数值.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:解答题
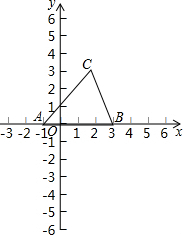 我们把一组对边平行且相等的四边形称为平行四边形,如图,在平面直角坐标系中,已知A(-1,0),B(3,0),C(2,3),你在坐标系内找一点D,使A,B,C,D形成一个平行四边形,你能找到几个这样的D点?画出所有情况的图形,并写出它们的坐标.
我们把一组对边平行且相等的四边形称为平行四边形,如图,在平面直角坐标系中,已知A(-1,0),B(3,0),C(2,3),你在坐标系内找一点D,使A,B,C,D形成一个平行四边形,你能找到几个这样的D点?画出所有情况的图形,并写出它们的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
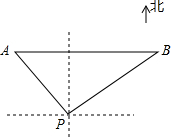 如图,小岛A位于港口P北偏西30°的方向,在小岛A的正东方向有一小岛B,小岛B位于港口P北偏东45°的方向,小岛A与港口P距离为20$\sqrt{3}$海里,则A,B两个小岛的距离为( )
如图,小岛A位于港口P北偏西30°的方向,在小岛A的正东方向有一小岛B,小岛B位于港口P北偏东45°的方向,小岛A与港口P距离为20$\sqrt{3}$海里,则A,B两个小岛的距离为( )| A. | 30海里 | B. | 30$\sqrt{3}$海里 | C. | 60海里 | D. | (30+10$\sqrt{3}$)海里 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$或$\frac{3}{4}$ | D. | -$\frac{4}{3}$或$\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
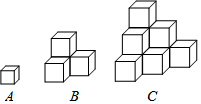
| 层数 | 1 | 2 | 3 | 4 | … | n |
| t | 1 | 3 | 6 | 10 | … | $\frac{n(n+1)}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com