
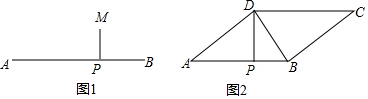
分析 (1)利用垂径定理结合相似三角形的判定与性质得出C点即可;
(2)将等积式PD2=AP•PB化为等比式,可得到△DAP∽△BDP,设AD=a,BD=b,AB=c,列出方程组即可解答.
解答 解:(1)如图所示:作AB的垂直平分线,以O为圆心,$\frac{1}{2}$AB为半径作圆,射线PM交⊙O于点C,C点即为所求.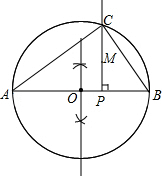
(2)∵PD2=AP•PB,
∴PD:AP=PB:PD,
又∵DP⊥AB于P,
∴∠DPA=∠DPB,
∴△DAP∽△BDP,
∴∠ADB=90°,
设AD=a,BD=b,AB=c,
由题意得,
$\left\{\begin{array}{l}{ab=48}\\{a+b+c=24}\\{{a}^{2}+{b}^{2}={c}^{2}}\end{array}\right.$,
解得,AB=c=10,
∵$\frac{1}{2}$DP•AB=$\frac{1}{2}$AD•DB=$\frac{1}{2}$×48=24,
∴PD=4.8.
点评 本题考查了相似三角形的判定与性质、平行四边形的性质,找到△DAP∽△BDP并利用相似三角形的性质找到相等的直角是解题的关键.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
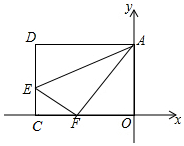 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(-10,8),则△AEF的面积为( )
如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(-10,8),则△AEF的面积为( )| A. | 15 | B. | 20 | C. | 25 | D. | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
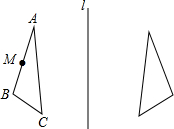 如图所示,在图形中标出点A、B、C关于直线l的对称点D、E、F.若M为AB的中点,在图中标出它的对称点N.若AB=10,AB边上的高为4,则△DEF的面积为多少?
如图所示,在图形中标出点A、B、C关于直线l的对称点D、E、F.若M为AB的中点,在图中标出它的对称点N.若AB=10,AB边上的高为4,则△DEF的面积为多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是丁丁画的一张脸的示意图,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
如图是丁丁画的一张脸的示意图,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )| A. | (1,0) | B. | (-1,0) | C. | (-1,1) | D. | (1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们刚刚学习的勾股定理是一个基本的平面几何定理,也是数学中最重要的定理之一.勾股定理其实有很多种方式证明.下图是1876年美国总统Garfield证明勾股定理所用的图形:
我们刚刚学习的勾股定理是一个基本的平面几何定理,也是数学中最重要的定理之一.勾股定理其实有很多种方式证明.下图是1876年美国总统Garfield证明勾股定理所用的图形:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com